第 10 章 循环神经网络
在前面两章中,我们分别介绍了神经网络的基础概念和最简单的MLP,以及适用于图像处理的CNN。从中我们可以意识到,不同结构的神经网络具有不同的特点,在不同任务上具有自己的优势。例如MLP复杂度低、训练简单、适用范围广,适合解决普通任务或作为大型网络的小模块;CNN可以捕捉到输入中不同尺度的关联信息,适合从图像中提取特征。而对于具有序列特征的数据,例如一年内随时间变化的温度、一篇文章中的文字等,它们具有明显的前后关联。然而这些关联的数据在序列中出现的位置可能间隔非常远,例如文章在开头和结尾描写了同一个事物,如果用CNN来提取这些关联的话,其卷积核的大小需要和序列的长度相匹配。当数据序列较长时,这种做法会大大增加网络复杂度和训练难度。因此,我们需要引入一种新的网络结构,使其能够充分利用数据的序列性质,从前到后分析数据、提取关联。这就是本章要介绍的循环神经网络(recurrent neural networks,RNN)。
10.1 循环神经网络的基本原理
我们先从最简单的模型开始考虑。对于不存在序列关系的数据,我们采用一个两层的MLP来拟合它,如图10-1(a)所示,输入样本为
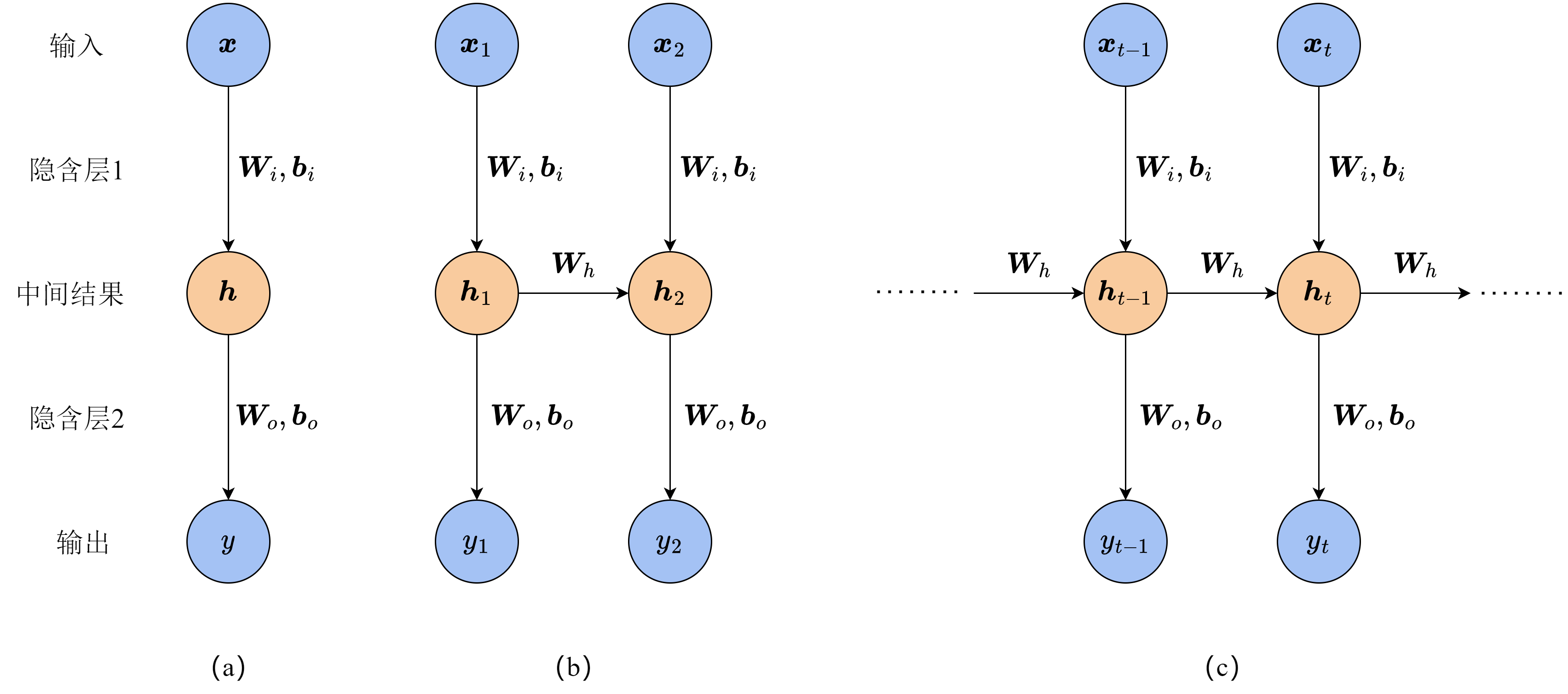
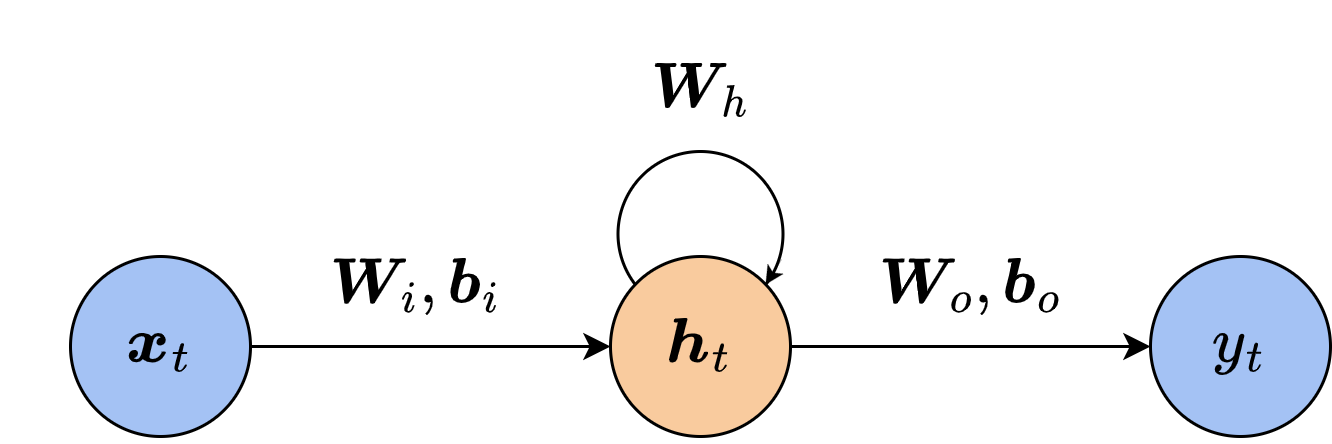
假设数据集中的数据分别是在时刻1和时刻2采集到的,并且我们知道时刻2的结果与时刻1有关。这时,由于两个时刻的数据产生了依赖关系,如果我们用相同的模型权重来进行预测而忽略其关联,预测的准确度就会降低。为了利用上额外的关联信息,我们将MLP的结构拓展一下,如图10-1(b)所示,第二个MLP的中间向量与一般的MLP不同。在计算时刻2的中间向量
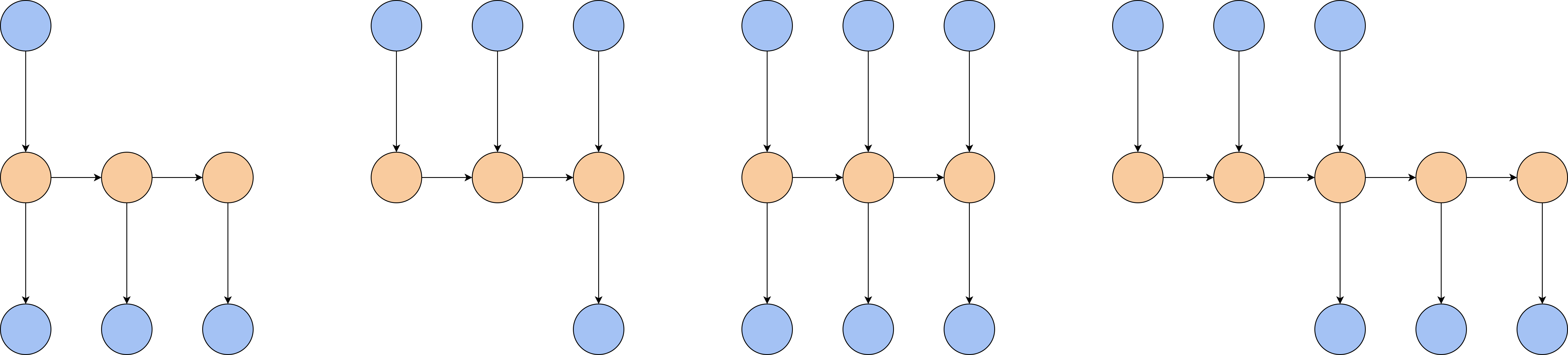
RNN的输入与输出并不一定要像上面展示的一样,在每一时刻都有一个输入样本和一个预测输出。根据任务的不同,RNN的输入输出对应可以有多种形式。图10-3展示了一些不同对应形式的RNN结构,从左到右依次是一对多、多对一、同步多对多和异步多对多,它们都有合适的任务场景。例如,如果我们要根据一个关键词生成一句话,以词语作为最小单元,那么RNN的输入只有一个,而生成的句子需要有连贯的含义和语义,因此可以利用RNN在每一时刻输出一个词,从前到后连成完整的句子。这样的任务就更适合采用一对多的结构。再比如,常见的时间序列预测任务需要我们根据一段时间中收集的数据,预测接下来一定时间内数据的情况。这时,我们就可以用异步多对多的结构,先分析样本的规律和特征,再生成紧接着样本所在时间之后的结果。
当我们训练RNN时,由于每一时刻的中间向量都会组合上一时刻的中间向量,如果把时刻
如果在
代入
观察上式可以发现,梯度中会出现一些
为了防止上述现象发生,最简单的做法是对梯度进行裁剪,为梯度设置上限和下限,当梯度过大或过小时,直接用上下限来代替梯度的值。但是,这种做法在复杂情况下仍然会导致信息丢失,通常只作为一种辅助手段。我们还可以选用合适的激活函数
10.2 门控循环单元
本节,我们就来介绍一种较为简单的设计——门控循环单元(gated recurrent unit,GRU)
图10-4展示了GRU单元的内部结构,GRU设置的门控单元共有两个,分别称为更新门和重置门。每个门控单元输出一个数值或向量,由上一时刻的信息
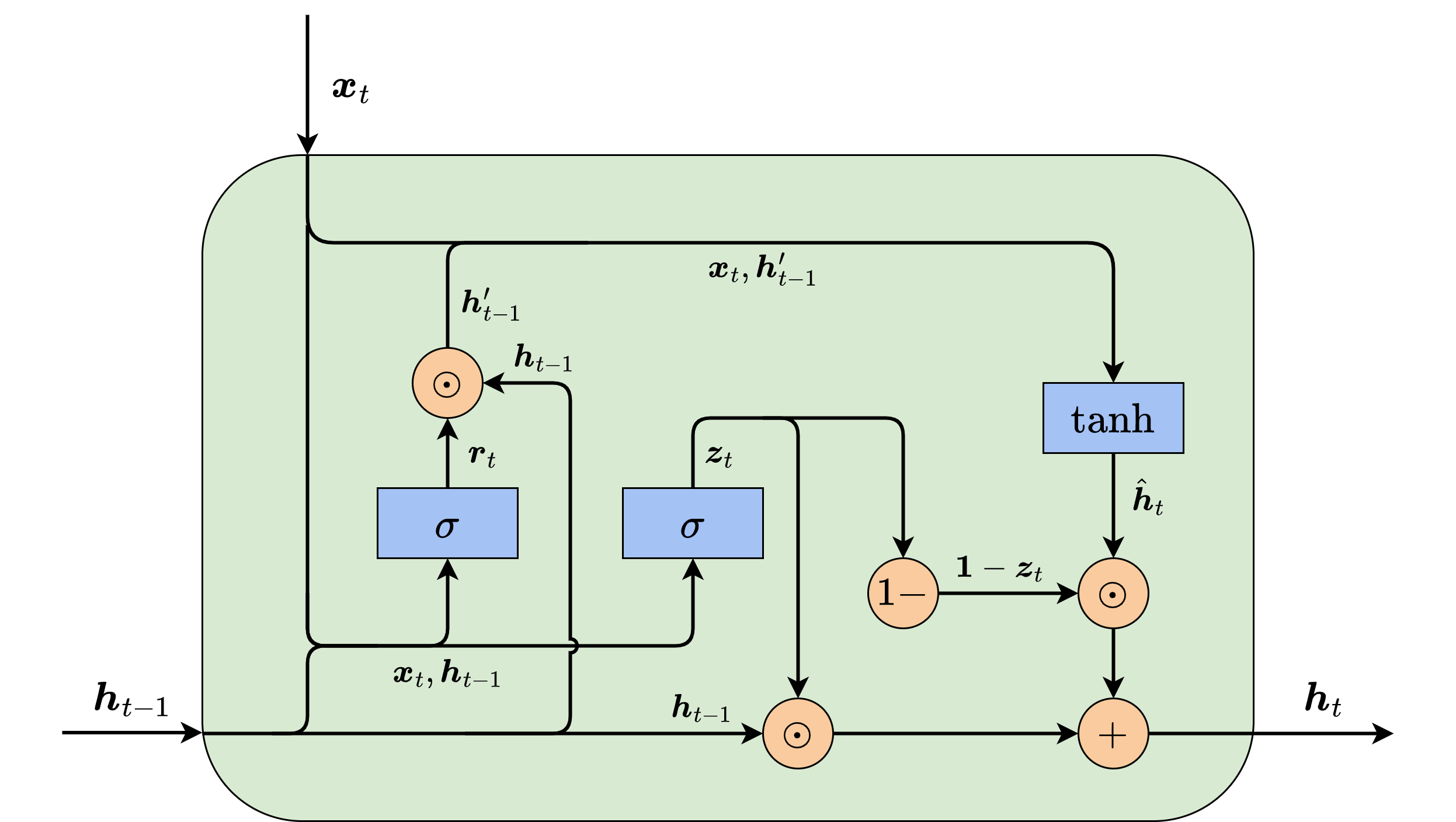
其中,
其中
当
这里得到的
最后,我们要决定
在上式中,如果更新单元
为什么GRU的设计可以缓解梯度爆炸与梯度消失问题呢?上文我们已经提到,导致梯度问题的最大因素是
虽然门控单元的值也是由网络训练得到的,但是门控单元的引入使得GRU可以自我调节梯度。也就是说,如果
10.3 动手实现GRU
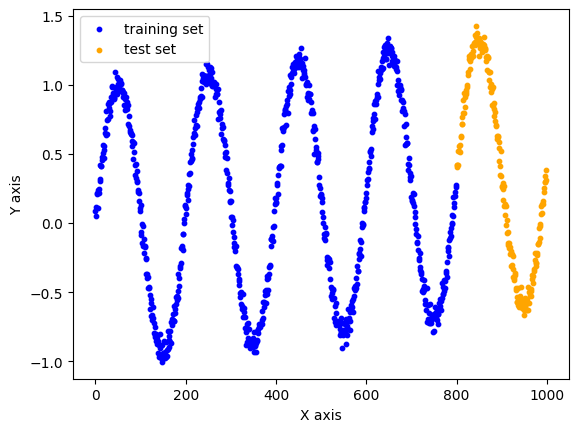
本节我们使用PyTorch库中的工具来实现GRU模型,完成简单的时间序列预测任务。时间序列预测任务是指根据一段连续时间内采集的数据、分析其变化规律、预测接下来数据走向的任务。如果当前数据与历史数据存在依赖关系,或者有随时间有一定的规律性,该任务就很适合用RNN求解。本节中,我们生成了一条经过一定处理的正弦曲线作为数据集,存储在sindata_1000.csv中。该曲线包含1000个数据点。其中前800个点作为训练集,后200个点作为测试集。由于本任务是时序预测任务,我们在划分训练集和测试集时无须将其打乱。我们首先导入必要的库和数据集,并将数据集的图像绘制出来。
import numpy as npimport matplotlib.pyplot as pltfrom tqdm import tqdmimport torchimport torch.nn as nn# 导入数据集data = np.loadtxt('sindata_1000.csv', delimiter=',')num_data = len(data)split = int(0.8 * num_data)print(f'数据集大小:{num_data}')# 数据集可视化plt.figure()plt.scatter(np.arange(split), data[:split],color='blue', s=10, label='training set')plt.scatter(np.arange(split, num_data), data[split:],color='orange', s=10, label='test set')plt.xlabel('X axis')plt.ylabel('Y axis')plt.legend()plt.show()# 分割数据集train_data = np.array(data[:split])test_data = np.array(data[split:])
数据集大小:1000
在训练RNN模型时,虽然我们可以把每个时间步
# 输入序列长度seq_len = 20# 处理训练数据,把切分序列后多余的部分去掉train_num = len(train_data) // (seq_len + 1) * (seq_len + 1)train_data = np.array(train_data[:train_num]).reshape(-1, seq_len + 1, 1)np.random.seed(0)torch.manual_seed(0)x_train = train_data[:, :seq_len] # 形状为(num_data, seq_len, input_size)y_train = train_data[:, 1: seq_len + 1]print(f'训练序列数:{len(x_train)}')# 转为PyTorch张量x_train = torch.from_numpy(x_train).to(torch.float32)y_train = torch.from_numpy(y_train).to(torch.float32)x_test = torch.from_numpy(test_data[:-1]).to(torch.float32)y_test = torch.from_numpy(test_data[1:]).to(torch.float32)
训练序列数:38
考虑到GRU的模型结构较为复杂,我们直接使用在PyTorch库中封装好的GRU模型。我们只需要为该模型提供两个参数,第一个参数input_size表示输入hidden_size表示中间向量out和hidden,前者是整个时间序列上中间变量的值,而后者只包含是最后一步。out[-1]和hidden在GRU内部的层数不同时会有区别,但本节只使用单层网络,因此不详细展开。感兴趣的读者可以参考PyTorch的官方文档。我们将out作为最后全连接层的输入,得到预测值,再把预测值和hidden返回。hidden将作为下一次前向传播的初始中间变量。
class GRU(nn.Module):# 包含PyTorch的GRU和拼接的MLPdef __init__(self, input_size, output_size, hidden_size):super().__init__()# GRU模块self.gru = nn.GRU(input_size=input_size, hidden_size=hidden_size)# 将中间变量映射到预测输出的MLPself.linear = nn.Linear(hidden_size, output_size)def forward(self, x, hidden):# 前向传播# x的维度为(batch_size, seq_len, input_size)# GRU模块接受的输入为(seq_len, batch_size, input_size)# 因此需要对x进行变换# transpose函数可以交换x的坐标轴# out的维度是(seq_len, batch_size, hidden_size)out, hidden = self.gru(torch.transpose(x, 0, 1), hidden)# 取序列最后的中间变量输入给全连接层out = self.linear(out.view(-1, hidden_size))return out, hidden
接下来,我们设置超参数并实例化GRU。在训练之前,我们还要强调时序模型在测试时与普通模型的区别。GRU在测试时,我们将输入的时间序列长度降为1,即只输入
# 超参数input_size = 1 # 输入维度output_size = 1 # 输出维度hidden_size = 16 # 中间变量维度learning_rate = 5e-4# 初始化网络gru = GRU(input_size, output_size, hidden_size)gru_optim = torch.optim.Adam(gru.parameters(), lr=learning_rate)# GRU测试函数,x和hidden分别是初始的输入和中间变量def test_gru(gru, x, hidden, pred_steps):pred = []inp = x.view(-1, input_size)for i in range(pred_steps):gru_pred, hidden = gru(inp, hidden)pred.append(gru_pred.detach())inp = gru_predreturn torch.concat(pred).reshape(-1)
作为对比,我们用相同的数据同步训练一个3层的MLP模型。该MLP将同样将
# MLP的超参数hidden_1 = 32hidden_2 = 16mlp = nn.Sequential(nn.Linear(input_size, hidden_1),nn.ReLU(),nn.Linear(hidden_1, hidden_2),nn.ReLU(),nn.Linear(hidden_2, output_size))mlp_optim = torch.optim.Adam(mlp.parameters(), lr=learning_rate)# MLP测试函数,相比于GRU少了中间变量def test_mlp(mlp, x, pred_steps):pred = []inp = x.view(-1, input_size)for i in range(pred_steps):mlp_pred = mlp(inp)pred.append(mlp_pred.detach())inp = mlp_predreturn torch.concat(pred).reshape(-1)
最后,我们用完全相同的数据训练GRU和MLP。由于已经有了序列长度,我们不再设置SGD的批量大小,直接将每个训练样本单独输入模型进行优化。
max_epoch = 150criterion = nn.functional.mse_losshidden = None # GRU的中间变量# 训练损失gru_losses = []mlp_losses = []gru_test_losses = []mlp_test_losses = []# 开始训练with tqdm(range(max_epoch)) as pbar:for epoch in pbar:st = 0gru_loss = 0.0mlp_loss = 0.0# 随机梯度下降for X, y in zip(x_train, y_train):# 更新GRU模型# 我们不需要通过梯度回传更新中间变量# 因此将其从有梯度的部分分离出来if hidden is not None:hidden.detach_()gru_pred, hidden = gru(X[None, ...], hidden)gru_train_loss = criterion(gru_pred.view(y.shape), y)gru_optim.zero_grad()gru_train_loss.backward()gru_optim.step()gru_loss += gru_train_loss.item()# 更新MLP模型# 需要对输入的维度进行调整,变成(seq_len, input_size)的形式mlp_pred = mlp(X.view(-1, input_size))mlp_train_loss = criterion(mlp_pred.view(y.shape), y)mlp_optim.zero_grad()mlp_train_loss.backward()mlp_optim.step()mlp_loss += mlp_train_loss.item()gru_loss /= len(x_train)mlp_loss /= len(x_train)gru_losses.append(gru_loss)mlp_losses.append(mlp_loss)# 训练和测试时的中间变量序列长度不同,训练时为seq_len,测试时为1gru_pred = test_gru(gru, x_test[0], hidden[:, -1], len(y_test))mlp_pred = test_mlp(mlp, x_test[0], len(y_test))gru_test_loss = criterion(gru_pred, y_test).item()mlp_test_loss = criterion(mlp_pred, y_test).item()gru_test_losses.append(gru_test_loss)mlp_test_losses.append(mlp_test_loss)pbar.set_postfix({'Epoch': epoch,'GRU loss': f'{gru_loss:.4f}','MLP loss': f'{mlp_loss:.4f}','GRU test loss': f'{gru_test_loss:.4f}','MLP test loss': f'{mlp_test_loss:.4f}'})
100%|██████████| 150/150 [00:42<00:00, 3.52it/s, Epoch=149, GRU loss=0.0034, MLP loss=0.0056, GRU test loss=0.0392, MLP test loss=1.1252]
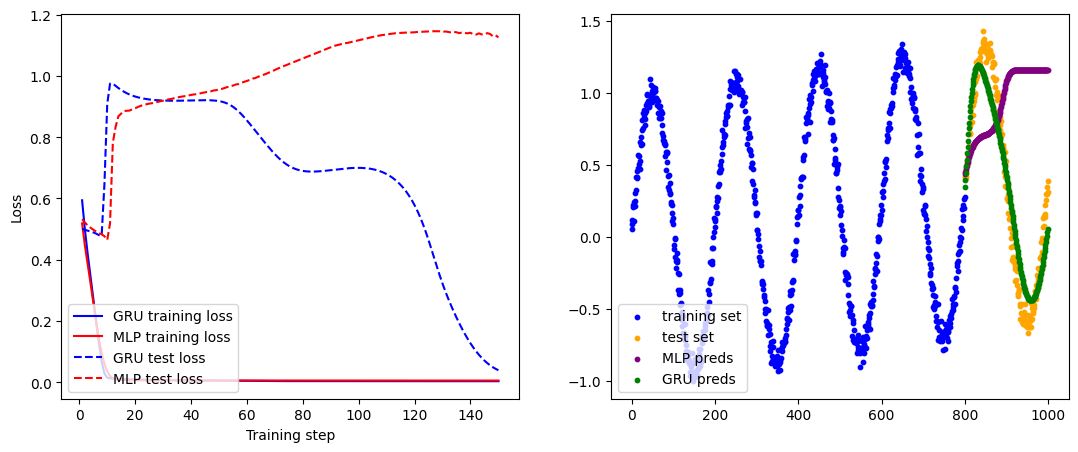
最后,我们在测试集上对比GRU和MLP模型的效果并绘制出来。图中包含了原始数据的训练集和测试集的曲线,可以看出,GRU的预测基本符合测试集的变化规律,而MLP很快就因为缺乏足够的时序信息与测试集偏离。
# 最终测试结果gru_preds = test_gru(gru, x_test[0], hidden[:, -1], len(y_test)).numpy()mlp_preds = test_mlp(mlp, x_test[0], len(y_test)).numpy()plt.figure(figsize=(13, 5))# 绘制训练曲线plt.subplot(121)x_plot = np.arange(len(gru_losses)) + 1plt.plot(x_plot, gru_losses, color='blue', label='GRU training loss')plt.plot(x_plot, mlp_losses, color='red', label='MLP training loss')plt.plot(x_plot, gru_test_losses, color='blue',linestyle='--', label='GRU test loss')plt.plot(x_plot, mlp_test_losses, color='red',linestyle='--', label='MLP test loss')plt.xlabel('Training step')plt.ylabel('Loss')plt.legend(loc='lower left')# 绘制真实数据与模型预测值的图像plt.subplot(122)plt.scatter(np.arange(split), data[:split], color='blue',s=10, label='training set')plt.scatter(np.arange(split, num_data), data[split:], color='orange',s=10,label='test set')plt.scatter(np.arange(split, num_data - 1), mlp_preds, color='purple',s=10, label='MLP preds')plt.scatter(np.arange(split, num_data - 1), gru_preds, color='green',s=10, label='GRU preds')plt.legend(loc='lower left')plt.show()
10.4 本章小结
本章主要介绍了循环神经网络及其变体门控循环单元,并在简单的数据集上实现了GRU模型。与其他的神经网络结构相比,RNN充分利用了数据中的序列特性,将中间向量按时间步不断向后传播,从而具有捕捉序列型关联的能力。然而在实际应用中,由于RNN的结构导致其梯度回传的表达式中出现参数的连乘,其较容易出现梯度消失和梯度爆炸等问题。许多RNN的改进算法通过设计中间变量传播中的函数
习题
以下关于RNN的说法不正确的是: A. RNN的权值更新通过与MLP相同的传统反向传播算法进行计算。 B. RNN的中间结果不仅取决于当前的输入,还取决于上一时间步的中间结果。 C. RNN结构灵活,可以控制输入输出的数目,以针对不同的任务。 D. RNN中容易出现梯度消失或梯度爆炸问题,因此很难应用在序列较长的任务上。
以下关于GRU的说法正确的是: A. GRU主要改进了RNN从中间结果到输出之间的结构,可以提升RNN的表达能力。 B. GRU相较于一般的RNN更为复杂,但训练反而更加简单。 C. 没有一种网络结构可以完整保留过去的所有信息,GRU只是合适的取舍方式。 D. 重置门和更新门的输入完全相同,因此可以合并为一个门。
在10.3动手实现GRU一节中,根据任务特点,我们用到的RNN的输入输出对应关系是什么?
GRU的重置门和更新门,哪个可以维护长期记忆?哪个可以捕捉短期信息?
基于本章的代码,调整RNN和GRU的输入序列长度并做同样的训练和测试,观察其模型性能随序列长度的变化情况。
PyTorch中还提供了封装好的LSTM工具
torch.nn.LSTM,使用方法与GRU类似。将本节代码中的GRU改为LSTM,对比两者的表现。
参考文献
[1] GRU论文:Cho K, Van Merriënboer B, Bahdanau D, et al. On the properties of neural machine translation: Encoder-decoder approaches[J]. arXiv preprint arXiv:1409.1259, 2014.
[2] LSTM论文:Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural computation, 1997, 9(8): 1735-1780.