第 16 章 概率图模型
本章讨论无监督学习中的数据分布建模问题。当我们需要在一个数据集上完成某个任务时,数据集中的样本分布显然是最基本的要素。面对不同的数据分布,我们可能针对同一任务采用完全不同的算法。例如,如果样本有明显的线性相关关系,我们就可以考虑用基于线性模型的算法解决问题;如果样本呈高斯分布,我们可能会使用高斯分布的各种性质来简化任务的要求。上一章介绍的数据降维算法,也是为了在数据分布不明显的前提下,尽可能提取出数据的关键特征。因此,如何建模数据集中样本关于其各个特征的分布,就成了一个相当关键的问题。
我们从图16-1的场景中看起。一群人在秋天出游,银杏满地,风光无限。但是,在同一个温度下,不同人的衣着也有差异。有人穿了厚厚的大衣,有人穿了长袖长裤,还有人穿着短袖或者裙子。可以设想,如果气温再高一些,穿短袖的人会增加;如果气温再低一些,恐怕就不会有人再穿短袖了。因此我们可以认为,人群穿衣选择的概率分布受到天气的影响。

我们先从最简单的表格数据看起。假设表16-1中是天气和人群中衣服选择的部分数据,我们可以直接从中写出最简单的数据分布:
表 16-1 不同天气和穿衣选择的概率
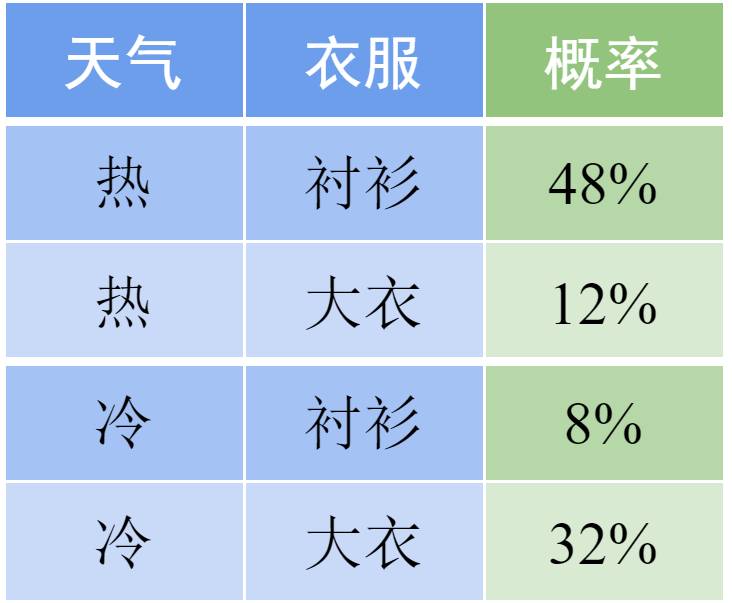
以此类推,我们可以把表中的每一行都写出来,得到样本的分布。但是,这样的做法显然过于低效。当特征的数目增加时,我们按此建模的复杂度将成指数增长。因此,我们需要设法寻找不同特征之间的相关性,降低模型的复杂度。例如,根据生活常识,我们可以认为人们选择衣服的概率应该是和天气有关的。天气热时,人们更倾向于选择衬衫,而天气冷时倾向于大衣。这样,我们可以将上面的分布转化为条件概率:
通过这种方式,我们可以建立起样本不同特征之间的关系。如果用随机变量
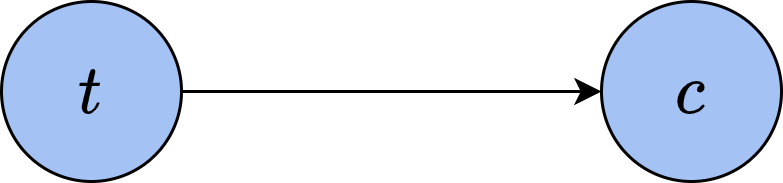
图中,从
16.1 贝叶斯网络
贝叶斯网络又称信念网络(belief network),与概率中的贝叶斯推断有很大关联。由于网络中的有向关系清楚地表明了变量间的依赖,我们可以根据网络结构直接写出变量的分布。例如,设变量
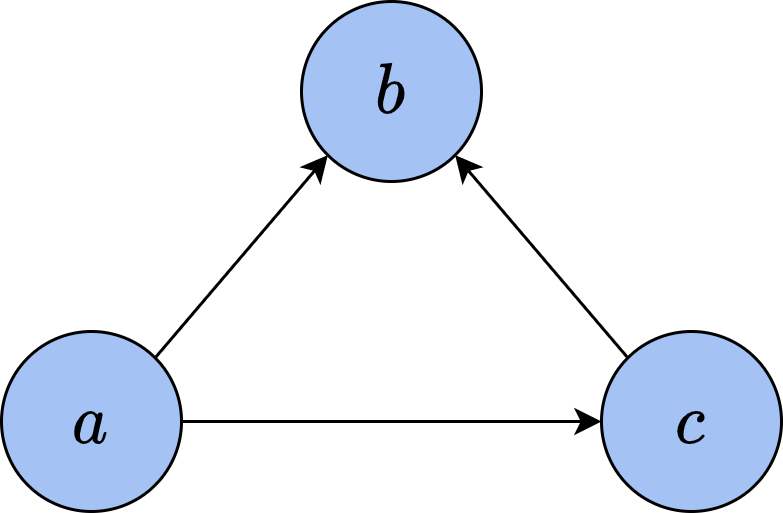
从图中可以看出,
对于一般的有
根据贝叶斯网络中,我们可以清晰地判断变量之间是否独立。如图16-4所示,我们以3个变量
从上式中我们并不能直接得到这些变量间的独立性。但是,如果给定变量
这说明变量
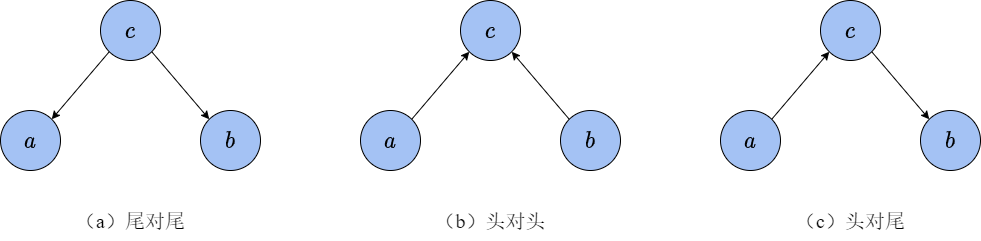
接下来我们考虑图16-4(b)展示的头对头关系。同样,可以根据图直接写出三者的联合分布
而根据条件概率公式,有
因此,这一情况中
这种情况似乎有些反直觉,为何原本独立的
表 16-2 带概率的逻辑与真值表
|
假如我们观测到
由于
这一结果说明,当观测到
最后我们来看16-5(c)的头对尾关系,这一关系比较好理解。首先,
当给定
因此
16.2 最大后验估计
在逻辑斯谛回归一章中,我们曾用最大似然估计的思想推导出了逻辑斯谛回归的优化目标。由于贝叶斯网络中的有向边清晰地表明了先验(prior)与后验(posterior)的关系,我们可以通过它推导出类似的结果。设数据集
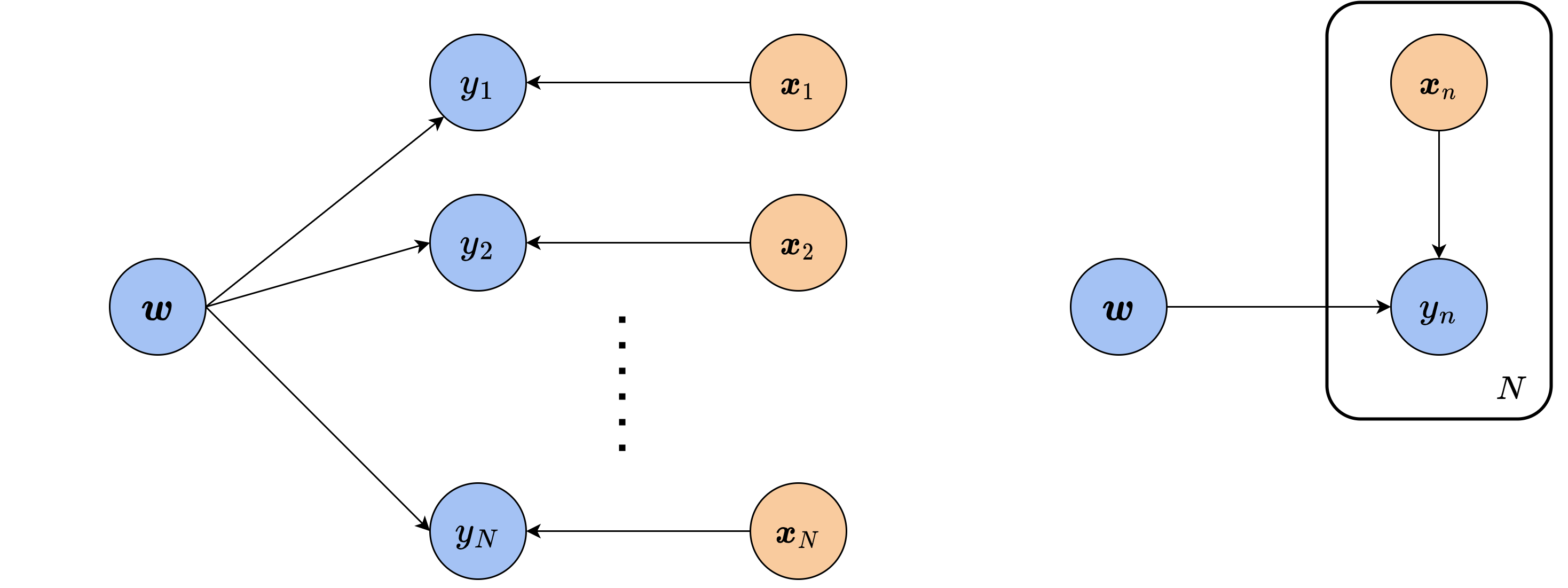
这里,图16-5(a)是完整的贝叶斯网络。可以看出,对每个样本和标签来说,它们之间的依赖关系都是相同的,在网络中表现为大量重复的结构。对于这样的重复,我们通常将其简写为图16-5(b)的形式,用一组
其中,参数自身的分布
上式中的分母
如果要进一步求解该后验分布,我们必须对参数空间和样本与标签之间的关系做出假设,以写出
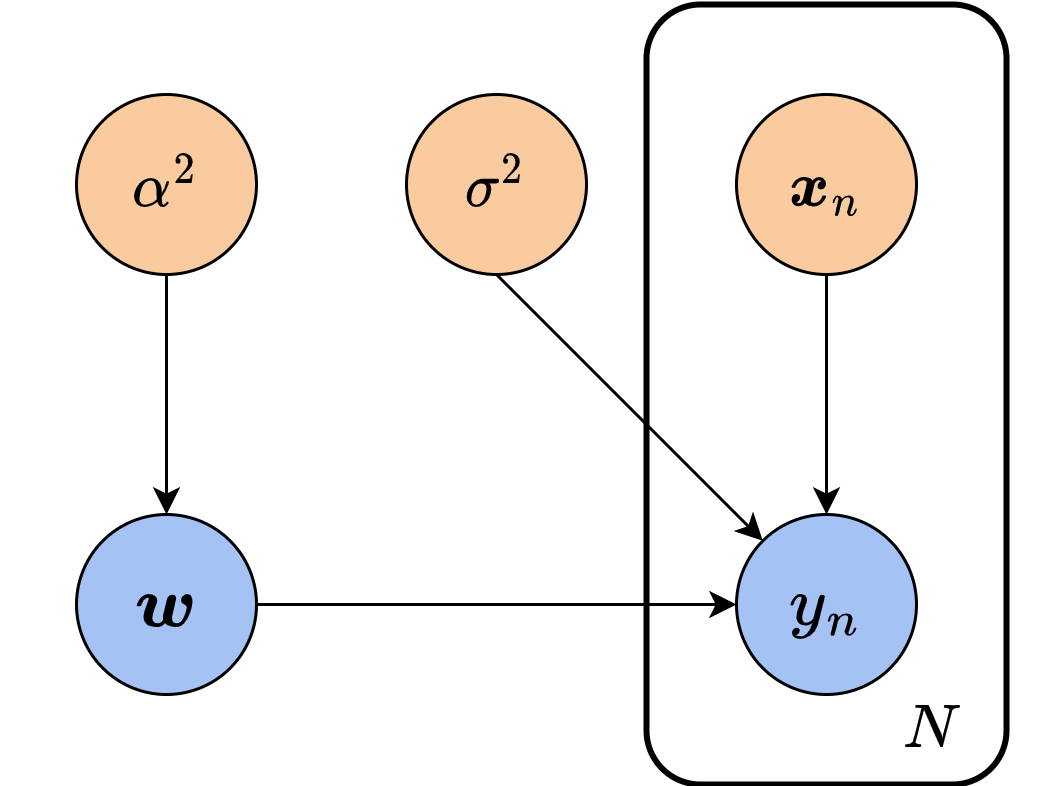
两个新引入的量都可以视为常量,因此在图中也用橙色节点表示。把上述的表达式代入后验分布,就得到:
设样本的维度是
与最大似然估计的思路类似,这里我们希望
因此,我们最终要解决的优化问题是:
可以发现,该目标函数与线性回归中用MSE损失函数、约束强度为
最大似然估计与最大后验估计是机器学习中常用的两种求解模型参数的方式,但两者有所不同。设数据集为
另一方面,MAP考虑最大化参数的后验分布
两者对比可以发现,MAP的优化目标比MLE多了一项
16.3 用朴素贝叶斯模型完成文本分类
朴素贝叶斯(naive Bayes)是贝叶斯公式和贝叶斯网络模型的最简单应用。顾名思义,朴素贝叶斯模型只使用基本的条件独立假设和计数方法,统计各个变量的先验分布,再由贝叶斯公式反推出参数的后验。应用到分类模型中,待求的参数就是每个样本的类别。设样本的特征是

这里,我们事实上隐含了各个特征之间相互独立的假设。具体来说,朴素贝叶斯模型假设:给定每个样本的类别
这样就有可以将特征变量的联合概率拆解为独立概率的乘积:
虽然这一假设在实际中不甚合理,但是作为最简单的朴素模型,这一假设可以大大简化我们计算的难度。下面,我们按与上节相同的步骤,在样本特征
式中
考虑到文本处理不属于本书的重点讲述范围,我们直接从sklearn中下载处理好的数据集,仅在这里简要介绍数据处理的方法。首先,我们将文本按照空白字符分隔成一个个单词,再将所有长度在(i,j) k表示矩阵第
import numpy as npfrom sklearn.datasets import fetch_20newsgroups_vectorizedfrom tqdm import trange# normalize表示是否对数据归一化,这里我们保留原始数据# data_home是数据保存路径train_data = fetch_20newsgroups_vectorized(subset='train',normalize=False, data_home='20newsgroups')test_data = fetch_20newsgroups_vectorized(subset='test',normalize=False, data_home='20newsgroups')print('文章主题:', '\n'.join(train_data.target_names))print(train_data.data[0])
文章主题: alt.atheismcomp.graphicscomp.os.ms-windows.misccomp.sys.ibm.pc.hardwarecomp.sys.mac.hardwarecomp.windows.xmisc.forsalerec.autosrec.motorcyclesrec.sport.baseballrec.sport.hockeysci.cryptsci.electronicssci.medsci.spacesoc.religion.christiantalk.politics.gunstalk.politics.mideasttalk.politics.misctalk.religion.misc(0, 56979) 4(0, 106171) 2(0, 129935) 2(0, 119977) 2(0, 106184) 3(0, 29279) 3(0, 111322) 1(0, 29403) 3(0, 123796) 6(0, 27618) 1(0, 92203) 2(0, 66608) 16(0, 86247) 6(0, 95392) 2(0, 101034) 1(0, 115475) 10(0, 47982) 1(0, 125053) 3(0, 76032) 1(0, 20228) 1(0, 29573) 1(0, 36979) 1(0, 40042) 1(0, 33764) 1(0, 43740) 2: :(0, 83940) 1(0, 92260) 1(0, 81998) 1(0, 106239) 1(0, 123430) 1(0, 52449) 1(0, 117029) 1(0, 114520) 1(0, 96088) 1(0, 125017) 1(0, 53572) 1(0, 89503) 1(0, 28948) 1(0, 6214) 1(0, 109025) 1(0, 29400) 1(0, 115508) 1(0, 76685) 1(0, 53320) 1(0, 107568) 1(0, 117020) 1(0, 108951) 1(0, 104352) 1(0, 80986) 1(0, 6216) 1
接下来,我们统计训练集中的
# 统计新闻主题频率cat_cnt = np.bincount(train_data.target)print('新闻数量:', cat_cnt)log_cat_freq = np.log(cat_cnt / np.sum(cat_cnt))# 对每个主题统计单词频率alpha = 1.0# 单词频率,20是主题个数,train_data.feature_names是分割出的单词log_voc_freq = np.zeros((20, len(train_data.feature_names))) + alpha# 单词计数,需要加上先验计数voc_cnt = np.zeros((20, 1)) + len(train_data.feature_names) * alpha# 用nonzero返回稀疏矩阵不为零的行列坐标rows, cols = train_data.data.nonzero()for i in trange(len(rows)):news = rows[i]voc = cols[i]cat = train_data.target[news] # 新闻类别log_voc_freq[cat, voc] += train_data.data[news, voc]voc_cnt[cat] += train_data.data[news, voc]log_voc_freq = np.log(log_voc_freq / voc_cnt)
新闻数量: [480 584 591 590 578 593 585 594 598 597 600 595 591 594 593 599 546 564465 377]100%|██████████| 1787565/1787565 [05:03<00:00, 5893.59it/s]
至此,统计的信息已经足够我们判断其他新闻的类型了。我们遍历所有主题
def test_news(news):rows, cols = news.nonzero()# 对数后验log_post = np.copy(log_cat_freq)for row, voc in zip(rows, cols):# 加上每个单词在类别下的后验log_post += log_voc_freq[:, voc]return np.argmax(log_post)
最后,我们在测试集的所有新闻上查看我们的分类准确率,只有当我们判断的类别与真实类别相同时才算作正确。
preds = []for news in test_data.data:preds.append(test_news(news))acc = np.mean(np.array(preds) == test_data.target)print('分类准确率:', acc)
分类准确率: 0.7823951141795008
在sklearn中也提供了朴素贝叶斯分类器,对于本例中的离散特征多分类任务,我们选用MultinomialNB进行测试,并与我们自己实现的效果比较。该分类器同样有默认参数
from sklearn.naive_bayes import MultinomialNBmnb = MultinomialNB(alpha=alpha)mnb.fit(train_data.data, train_data.target)print('分类准确率:', mnb.score(test_data.data, test_data.target))
分类准确率: 0.7728359001593202
16.4 马尔可夫网络
与贝叶斯网络不同,某些情况下,变量之间的关联是双向的。例如在KNN一章中,我们曾用到了照片中某一像素和周围像素大概率很接近这一假设。如果把每个像素看作一个变量,那么它和周围的像素就是互相影响、互相依赖的。这时,我们可以把贝叶斯网络的有向图变为无向图,构造出马尔可夫网络。
图16-8展示了一个简单的马尔可夫网络,其中包含5个变量
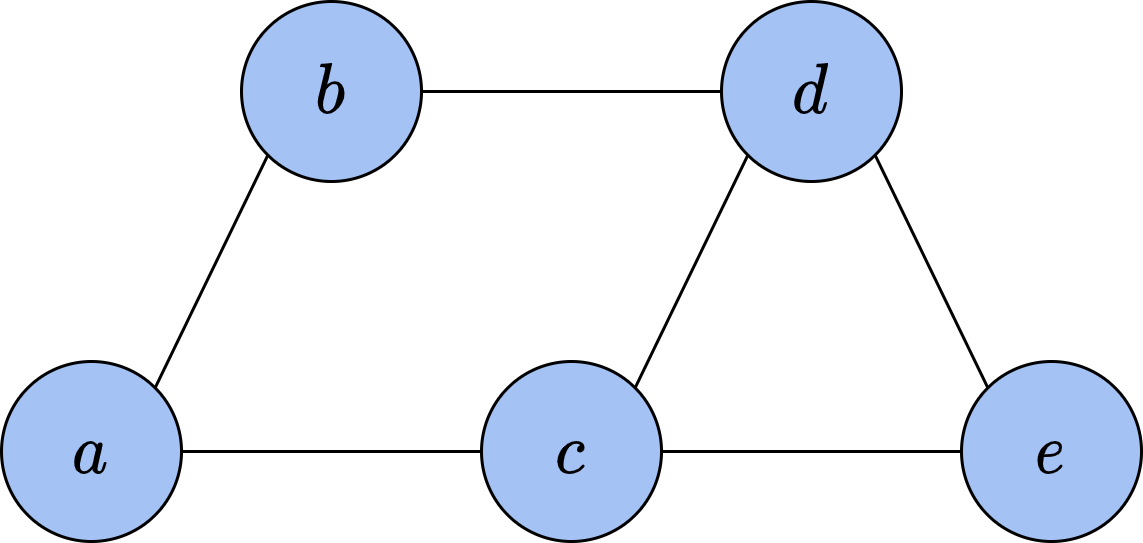
我们可以从这一性质出发,继续考虑马尔可夫网络的拆分。对于网络中的任意两个不同节点
如果变量
在图论中,如果一张无向图中的某些节点之间两两互相连接,我们就称这些节点组成了一个团(clique)。在图16-8中,大小为2的团有6个,分别是
记团
上式中的乘积遍历所有极大团,
由于概率分布必须处处非负,所有的函数
会让变量
如果势函数不仅非负,而且严格为正,我们可以用能量函数
再利用我们已经多次使用过的求对数的技巧,将寻找
该优化问题是对所有极大团的能量的和进行优化,且能量函数的取值和形式没有限制,相比于直接求解势函数的乘积方便很多。这一思想来自于物理中的势和势能,以及玻尔兹曼分布,感兴趣的读者可以自行查阅相关资料。下面,我们以图像去噪为例,展示马尔可夫网络的一个简单应用。
16.5 用马尔可夫网络完成图像去噪
上面我们已经讲过,对于一张有意义的图像,其每个像素点的颜色和周围像素点大概率相近,并且这一关联是双向的,符合马尔可夫网络的模型。当一张图像中存在噪点时,它们与周围像素的关联大概率比真实像素弱,反映在能量函数上,其整体的能量应当较大。因此,我们可以通过设计合适的能量函数并在图像上进行优化,还原出噪点的真实颜色。
简单起见,我们用一张只有两种颜色的图像来演示。如图16-9所示,上半部分是只有黑色与白色的原始图像,我们随机将其中10%的像素进行黑白反转,得到了下半部分带有噪声的图像。


为了对图像添加噪声前后的状态建模,设图像上像素的真实颜色
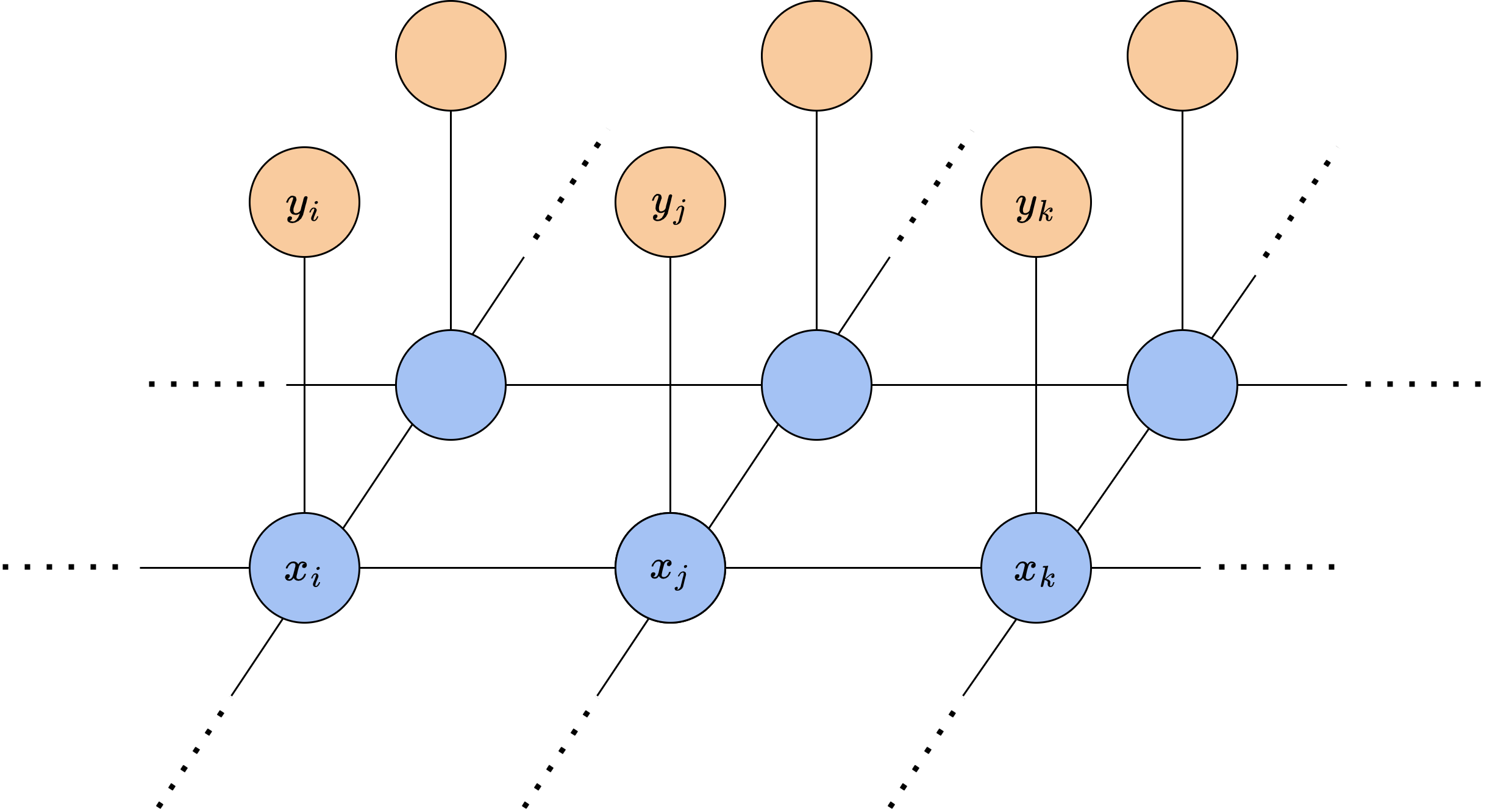
首先考虑真实像素间的关联,我们预计相邻的像素应当较为相似。由于图像中只有两种颜色-1和1,我们可以用相邻像素颜色的乘积
其中
这里
式中的第一项由于相邻像素对的能量被计算了两遍,额外乘上了
由于图像中像素数量
import matplotlib.image as mpimgimport matplotlib.pyplot as plt# 读取原图orig_img = np.array(mpimg.imread('origimg.jpg'), dtype=int)orig_img[orig_img < 128] = -1 # 黑色设置为-1orig_img[orig_img >= 128] = 1 # 白色设置为1# 读取带噪图像noisy_img = np.array(mpimg.imread('noisyimg.jpg'), dtype=int)noisy_img[noisy_img < 128] = -1noisy_img[noisy_img >= 128] = 1
为了在后续过程中计算去噪的效果,我们定义一个函数来计算当前图像与原图中不一致的像素比例。
def compute_noise_rate(noisy, orig):err = np.sum(noisy != orig)return err / orig.sizeinit_noise_rate = compute_noise_rate(noisy_img, orig_img)print (f'带噪图像与原图不一致的像素比例:{init_noise_rate * 100:.4f}%')
带噪图片与原图不一致的像素比例:9.9386%
由于图像在计算机中本身就是用二维数组存储,其结构与我们设计的马尔可夫网络相同,我们不需要再额外实现数据结构来存储马尔可夫网络。下面,我们就来直接实现逐像素优化的算法。在该算法中,优化每个像素时,能量的改变都是局部的。因此,我们只需要计算局部的能量变化,无须每次都重新计算整个网络的能量。
# 计算坐标(i, j)处的局部能量def compute_energy(X, Y, i, j, alpha, beta):# X:当前图像# Y:带噪图像energy = -beta * X[i][j] * Y[i][j]# 判断坐标是否超出边界if i > 0:energy -= alpha * X[i][j] * X[i - 1][j]if i < X.shape[0] - 1:energy -= alpha * X[i][j] * X[i + 1][j]if j > 0:energy -= alpha * X[i][j] * X[i][j - 1]if j < X.shape[1] - 1:energy -= alpha * X[i][j] * X[i][j + 1]return energy
最后,我们定义超参数,并将图像去噪结果随训练轮数的变化绘制出来。可以看出,随着迭代进行,图中在大范围色块内的噪点基本都消失了。
# 设置超参数alpha = 2.1beta = 1.0max_iter = 5# 逐像素优化# 复制一份噪声图像,保持网络中的Y不变,只优化XX = np.copy(noisy_img)for k in range(max_iter):for i in range(X.shape[0]): # 枚举所有像素for j in range(X.shape[1]):# 分别计算当前像素取1和-1时的能量X[i, j] = 1pos_energy = compute_energy(X, noisy_img, i, j, alpha, beta)X[i, j] = -1neg_energy = compute_energy(X, noisy_img, i, j, alpha, beta)# 将该像素设置为使能量最低的值X[i, j] = 1 if pos_energy < neg_energy else -1# 展示图像并计算噪声率plt.figure()plt.axis('off')plt.imshow(X, cmap='binary_r')plt.show()noise_rate = compute_noise_rate(X, orig_img) * 100print(f'迭代轮数:{k},噪声率:{noise_rate:.4f}%')

迭代轮数:0,噪声率:0.5632%

迭代轮数:1,噪声率:0.4071%

迭代轮数:2,噪声率:0.3993%

迭代轮数:3,噪声率:0.3979%

迭代轮数:4,噪声率:0.3975%
如果图像的图案更复杂、色彩更丰富,我们也可以使用类似的方法去噪,但是通常需要我们使用先验知识,设计更复杂的网络结构和能量函数。例如考虑彩色图像中的颜色渐变、考虑更大范围像素之间的关联等。在上例中,当黑色与白色给出的能量相同时,我们默认将其设置为白色。对于更复杂的情况,我们可以为每个像素单独设置一个能量函数
16.4 本章小结
本章仅介绍了概率图模型中最基本概念,它作为一种机器学习建模工具,具有广阔的应用范围。读者可以参阅《模式识别与机器学习》
习题
以下关于概率图模型的说法错误的是: A. 图分有向图和无向图两种,分别表示变量间的单向和双向依赖关系。 B. 概率图的有效建立往往需要人的先验知识。 C. 贝叶斯网络导出的MAP和MLE解是等价的。 D. 马尔可夫网络中势能越高的状态出现的概率越低。
以下关于条件独立的说法,不正确的是? A. 条件独立的定义是:考虑3个变量
假设给定 和 的情况下, 的条件分布不依赖于 的值,则在给定 的情况下 条件独立于 。 B. 图模型中的尾对尾结构中,当父节点未被观测到时,其子节点之间将不会条件独立 C. 图模型中的头对尾结构中,当中间节点未被观测到时,其两头的节点之间将不会条件独立 D. 图模型中的头对头结构中,当子节点未被观测到时,其父节点之间将不会条件独立 在线性模型中,假设参数
的先验分布是偏移参数为 、尺度参数为 的拉普拉斯分布,其概率密度函数为
仿照 16.1 节中的推导,利用MAP求解此时的优化目标。这个目标相当于为线性模型添加了什么正则化约束?
把一句话中的每个词看作一个单元,为了构成完整的具有语义的句子,这些单元之间必然存在关联。这种关联用哪种概率模型描述更合适?简要画出相应的概率图。
如果要扩展图像去噪中像素之间的关联,认为任意一个像素和周围的8个像素有关,对应的马尔可夫网络和能量函数要怎样变化?修改相应的代码,观察去噪结果是否有变化。
在20 newsgroups数据集中,各个新闻事实上还包含了标题、脚注、引用等信息,而这些信息常常含有大量提示主题的关键词。因此,是否包含这些信息对分类准确率的影响非常大。阅读文档,在
fetch_20newsgroups_vectorized函数中添加remove参数,把相关的主题信息移除,观察分类准确率的变化。在现实场景中,我们是否能获取到这些信息?这提示我们在利用机器学习完成实际中的任务时要注意什么?
参考文献
[1] 《模式识别与机器学习》:Bishop C M, Nasrabadi N M. Pattern recognition and machine learning[M]. New York: springer, 2006.
[2] 《概率图模型:原理与技巧》:Koller D, Friedman N. Probabilistic graphical models: principles and techniques[M]. MIT press, 2009.