第 11 章 支持向量机
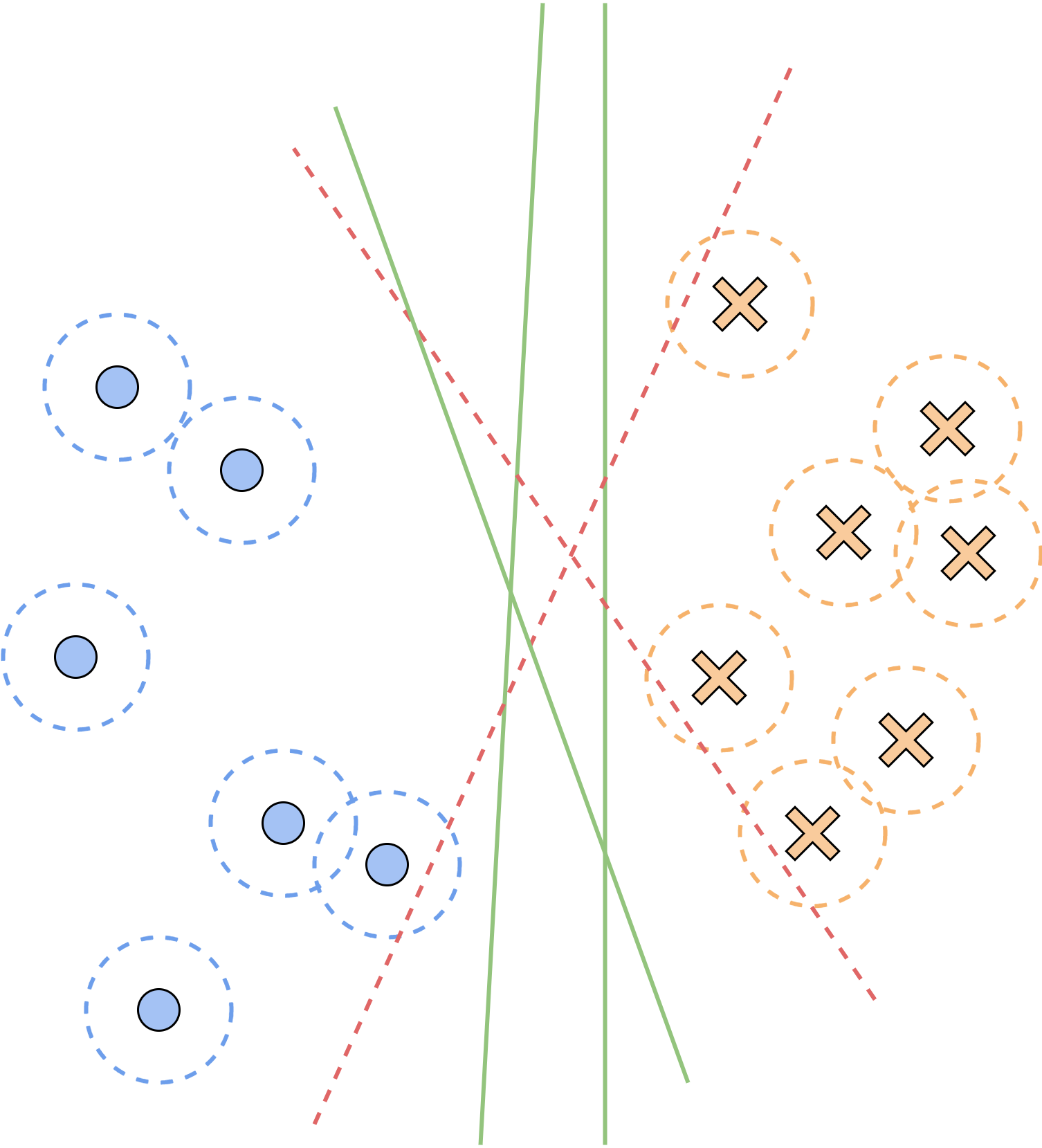
本章开始,我们介绍非参数化模型。与参数化模型不同,非参数化模型对数据分布不做先验的假设,从而能够更灵活地适配到不同的数据分布上。但另一方面,灵活性也使其对数据更为敏感,容易出现过拟合现象。本章主要介绍一个经典的非参数化模型:支持向量机(support vector machine,SVM),以及其求解算法序列最小优化(sequential minimal optimization,SMO)算法,并利用其完成平面点集的二分类任务。
由于非参数化模型与数据集大小有关,我们假设数据集
通常来说,即使数据集
11.1 支持向量机的数学描述
我们首先来考虑如何计算样本点与平面的间隔。如图11-2所示,设决策边界给出的超平面方程为
或者
出现两个不同的方程是因为我们还没有确定
或者等价变形为
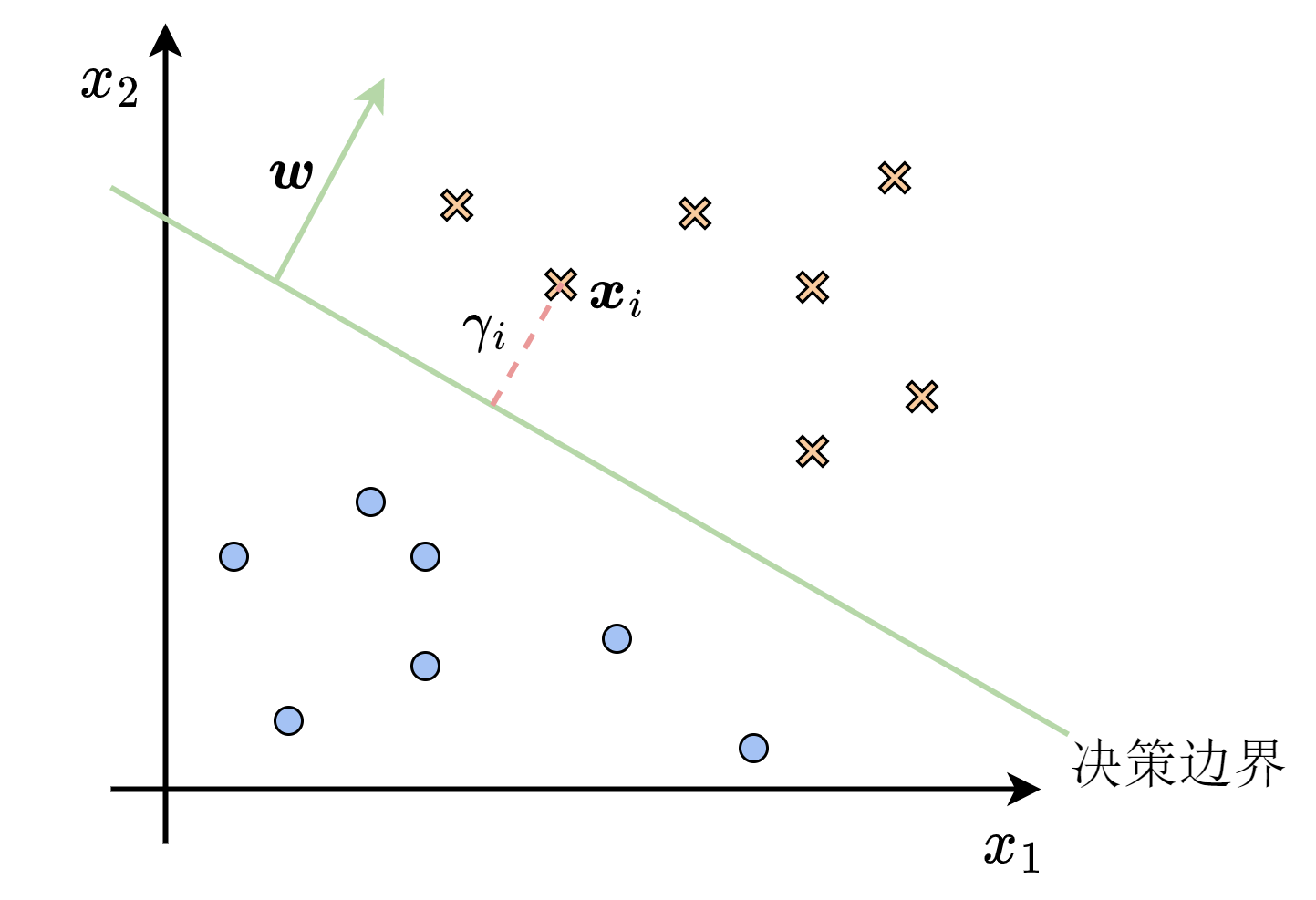
对上式来说,当
我们希望所有样本到平面的几何间隔
上面已经提到,函数间隔
然而,优化目标
由于
至此,我们讨论了数据线性可分的情况。如果数据线性不可分,我们可以适当放低上面的约束要求,引入松弛变量
可以看出,松弛变量允许某个样本点的类别与超平面给出的分类不同。但是,对这些分类错误的样本点,我们也需要进行惩罚。因此,我们在优化的目标函数上加入
对于带约束的凸优化问题,数学上有一套成熟的解决方式,将其转化为更容易的对偶问题求解。我们将较为繁琐的数学推导放在本章的拓展阅读中,感兴趣的读者可以自行学习,这里我们直接给出结论。求解上面的优化问题等价于求解下面的二次规划:
其中
当解出最优的
并且,这组最优参数
设支持向量的集合为
这样,用SVM进行预测的时间复杂度从
现在,我们只需要从上面的二次规划问题中解出
11.2 序列最小优化
序列最小优化的核心思想是,同时优化所有的参数
固定
其中
第二个约束条件表明,
将上式代入优化目标消去
其中,
如果数据集中没有相同的样本,那么严格有
其对应的大致图像如图11-3所示。
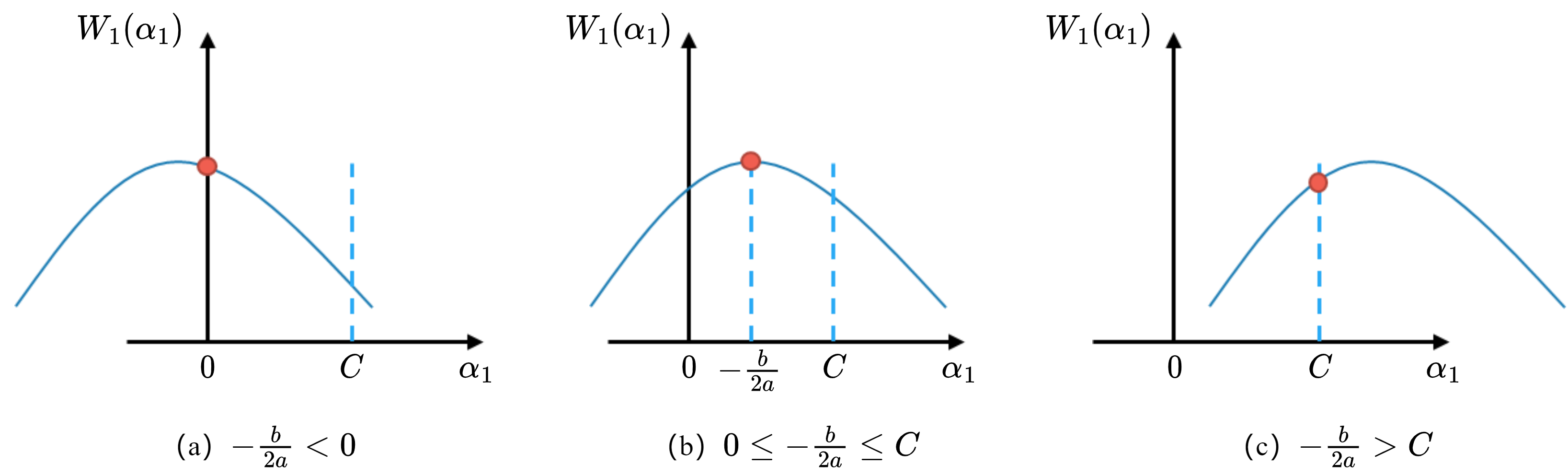
解出
为了代码实现方便,我们进一步化简
将
于是可得:
这一形式更加简洁和对称。
在计算出
同理,当
而如果
最后,我们将更新后的
11.3 动手实现SMO求解SVM
下面,我们按照上节讲述的步骤来动手实现SMO算法求解SVM。我们先考虑最简单的线性可分的情况,本节的数据集linear.csv包含了一些平面上的点及其分类。数据文件的每一行有3个数,依次是点的横坐标
import numpy as npimport matplotlib.pyplot as pltfrom matplotlib.colors import ListedColormapfrom tqdm import tqdm, trangedata = np.loadtxt('linear.csv', delimiter=',')print('数据集大小:', len(data))x = data[:, :2]y = data[:, 2]# 数据集可视化plt.figure()plt.scatter(x[y == -1, 0], x[y == -1, 1], color='red', label='y=-1')plt.scatter(x[y == 1, 0], x[y == 1, 1], color='blue', marker='x', label='y=1')plt.xlabel(r'$x_1$')plt.ylabel(r'$x_2$')plt.legend()plt.show()
数据集大小: 200
下面我们来实现SVM的主要部分SMO算法,具体的讲解放在代码注释中。
def SMO(x, y, ker, C, max_iter):'''SMO算法x,y:样本的值和类别ker:核函数,与线性回归中核函数的含义相同C:惩罚系数max_iter:最大迭代次数'''# 初始化参数m = x.shape[0]alpha = np.zeros(m)b = 0# 预先计算所有向量的两两内积,减少重复计算K = np.zeros((m, m))for i in range(m):for j in range(m):K[i, j] = ker(x[i], x[j])for l in trange(max_iter):# 开始迭代for i in range(m):# 有m个参数,每一轮迭代中依次更新# 固定参数alpha_i与另一个随机参数alpha_j,并且保证i与j不相等j = np.random.choice([l for l in range(m) if l != i])# 用-q/2p更新alpha_i的值eta = K[j, j] + K[i, i] - 2 * K[i, j] # 分母e_i = np.sum(y * alpha * K[:, i]) + b - y[i] # 分子e_j = np.sum(y * alpha * K[:, j]) + b - y[j]alpha_i = alpha[i] + y[i] * (e_j - e_i) / (eta + 1e-5) # 防止除以0zeta = alpha[i] * y[i] + alpha[j] * y[j]# 将alpha_i和对应的alpha_j保持在[0,C]区间# 0 <= (zeta - y_j * alpha_j) / y_i <= Cif y[i] == y[j]:lower = max(0, zeta / y[i] - C)upper = min(C, zeta / y[i])else:lower = max(0, zeta / y[i])upper = min(C, zeta / y[i] + C)alpha_i = np.clip(alpha_i, lower, upper)alpha_j = (zeta - y[i] * alpha_i) / y[j]# 更新bb_i = b - e_i - y[i] * (alpha_i - alpha[i]) * K[i, i] - y[j] * (alpha_j - alpha[j]) * K[i, j]b_j = b - e_j - y[j] * (alpha_j - alpha[j]) * K[j, j] - y[i] * (alpha_i - alpha[i]) * K[i, j]if 0 < alpha_i < C:b = b_ielif 0 < alpha_j < C:b = b_jelse:b = (b_i + b_j) / 2# 更新参数alpha[i], alpha[j] = alpha_i, alpha_jreturn alpha, b
利用SMO算法解出
# 设置超参数C = 1e8 # 由于数据集完全线性可分,我们不引入松弛变量max_iter = 1000np.random.seed(0)alpha, b = SMO(x, y, ker=np.inner, C=C, max_iter=max_iter)
0%| | 0/1000 [00:00<?, ?it/s]100%|██████████| 1000/1000 [00:16<00:00, 59.85it/s]
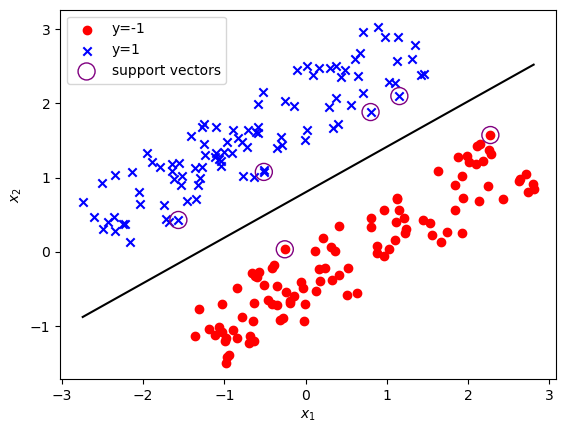
# 用alpha计算w,b和支持向量sup_idx = alpha > 1e-5 # 支持向量的系数不为零print('支持向量个数:', np.sum(sup_idx))w = np.sum((alpha[sup_idx] * y[sup_idx]).reshape(-1, 1) * x[sup_idx], axis=0)print('参数:', w, b)# 绘图X = np.linspace(np.min(x[:, 0]), np.max(x[:, 0]), 100)Y = -(w[0] * X + b) / (w[1] + 1e-5)plt.figure()plt.scatter(x[y == -1, 0], x[y == -1, 1], color='red', label='y=-1')plt.scatter(x[y == 1, 0], x[y == 1, 1], marker='x', color='blue', label='y=1')plt.plot(X, Y, color='black')# 用圆圈标记出支持向量plt.scatter(x[sup_idx, 0], x[sup_idx, 1], marker='o', color='none',edgecolor='purple', s=150, label='support vectors')plt.xlabel(r'$x_1$')plt.ylabel(r'$x_2$')plt.legend()plt.show()
支持向量个数: 6参数: [-1.0211867 1.66445549] -1.3343767573871523
11.4 核函数
对于略微有些线性不可分的数据,我们采用松弛变量的方法,仍然可以导出SVM的分隔超平面。然而,当数据的分布更加偏离线性时,可能完全无法用线性的超平面进行有效分类,松弛变量也就失效了。为了更清晰地展示非线性的情况,我们读入双螺旋数据集spiral.csv并绘制数据分布。该数据集包含了在平面上呈螺旋分布的两组点,同类的点处在同一条旋臂上。
data = np.loadtxt('spiral.csv', delimiter=',')print('数据集大小:', len(data))x = data[:, :2]y = data[:, 2]# 数据集可视化plt.figure()plt.scatter(x[y == -1, 0], x[y == -1, 1], color='red', label='y=-1')plt.scatter(x[y == 1, 0], x[y == 1, 1], marker='x', color='blue', label='y=1')plt.xlabel(r'$x_1$')plt.ylabel(r'$x_2$')plt.legend()plt.axis('square')plt.show()
数据集大小: 194
显然,平面上任意一条直线都无法为上图的双螺旋数据集给出分类。因此,我们需要引入非线性的特征映射。在神经网络一章中我们已经提到,非线性函数可以使数据升维,将在低维中线性不可分的数据映射到高维空间,使其变得线性可分。设映射函数为
为了简化上式,我们利用核技巧,定义核函数
虽然我们不知道
从而
实践中,
现在,我们的任务就变成寻找合适的核函数,来让原本线性不可分的数据线性可分。通常来说,核函数应当衡量向量之间的相似度。常用的核函数有:
- 内积核:
- 简单多项式核:
- 高斯核:
- 余弦相似度核:
- Sigmoid核:
下面,我们尝试用不同的非线性核函数对螺旋数据集进行分类,并观察分类效果。首先,我们实现上文介绍的几个核函数。
# 简单多项式核def simple_poly_kernel(d):def k(x, y):return np.inner(x, y) ** dreturn k# RBF核def rbf_kernel(sigma):def k(x, y):return np.exp(-np.inner(x - y, x - y) / (2.0 * sigma ** 2))return k# 余弦相似度核def cos_kernel(x, y):return np.inner(x, y) / np.linalg.norm(x, 2) / np.linalg.norm(y, 2)# sigmoid核def sigmoid_kernel(beta, c):def k(x, y):return np.tanh(beta * np.inner(x, y) + c)return k
然后,我们依次用这4种核函数计算SVM在双螺旋数据集上的分类结果。其中,简单多项式核取
kernels = [simple_poly_kernel(3),rbf_kernel(0.1),cos_kernel,sigmoid_kernel(1, -1)]ker_names = ['Poly(3)', 'RBF(0.1)', 'Cos', 'Sigmoid(1,-1)']C = 100max_iter = 500# 绘图准备,构造网格np.random.seed(0)plt.figure()fig, axs = plt.subplots(2, 2, figsize=(10, 10))axs = axs.flatten()cmap = ListedColormap(['coral', 'royalblue'])# 开始求解 SVMfor i in range(len(kernels)):print('核函数:', ker_names[i])alpha, b = SMO(x, y, kernels[i], C=C, max_iter=max_iter)sup_idx = alpha > 1e-6 # 支持向量的系数不为零sup_x = x[sup_idx] # 支持向量sup_y = y[sup_idx]sup_alpha = alpha[sup_idx]# 用支持向量计算 w^T*xdef wx(x_new):s = 0for xi, yi, ai in zip(sup_x, sup_y, sup_alpha):s += yi * ai * kernels[i](xi, x_new)return s# 构造网格并用 SVM 预测分类G = np.linspace(-1.5, 1.5, 100)G = np.meshgrid(G, G)X = np.array([G[0].flatten(), G[1].flatten()]).T # 转换为每行一个向量的形式Y = np.array([wx(xi) + b for xi in X])Y[Y < 0] = -1Y[Y >= 0] = 1Y = Y.reshape(G[0].shape)axs[i].contourf(G[0], G[1], Y, cmap=cmap, alpha=0.5)# 绘制原数据集的点axs[i].scatter(x[y == -1, 0], x[y == -1, 1], color='red', label='y=-1')axs[i].scatter(x[y == 1, 0], x[y == 1, 1], marker='x', color='blue', label='y=1')axs[i].set_title(ker_names[i])axs[i].set_xlabel(r'$x_1$')axs[i].set_ylabel(r'$x_2$')axs[i].legend()plt.tight_layout()plt.savefig('output_24_2.png')plt.savefig('output_24_2.pdf')plt.show()
核函数: Poly(3)100%|██████████| 500/500 [00:07<00:00, 66.05it/s]核函数: RBF(0.1)100%|██████████| 500/500 [00:07<00:00, 63.08it/s]核函数: Cos100%|██████████| 500/500 [00:08<00:00, 59.20it/s]核函数: Sigmoid(1,-1)100%|██████████| 500/500 [00:08<00:00, 58.54it/s]<Figure size 640x480 with 0 Axes>
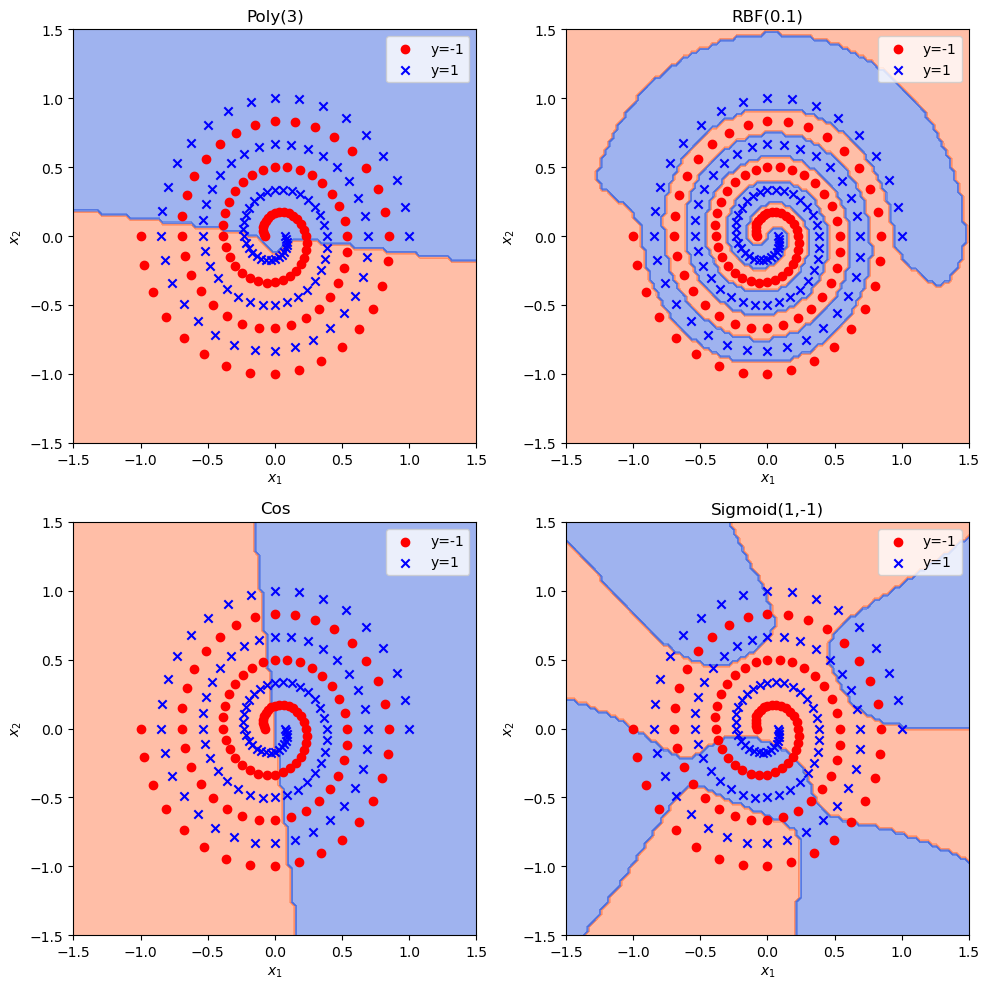
从实验结果图我们可以看出,不同的核函数对SVM模型的分类效果是截然不同的。对于双螺旋数据的二分类任务,高斯核函数(RBF)带给SVM的性能要明显好于其他核函数。根据高斯核函数的公式,我们可以看到高斯核本质是在衡量样本和样本之间基于欧几里得距离的相似度,这样使得欧几里得距离近的样本更好的聚在一起,在高维空间中达到线性可分。此外,松弛变量带来的对错分类样本的容忍度
11.5 Sklearn中的SVM工具
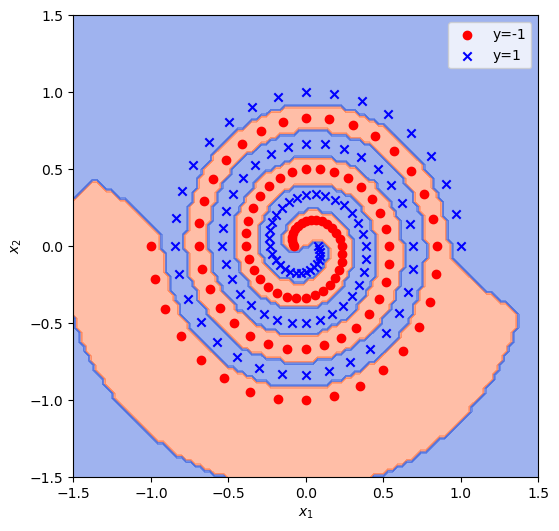
机器学习工具库sklearn提供了封装好的SVM工具,且支持多种内置核函数。我们以RBF核函数为例,复现上面在双螺旋数据集上的分类结果。在sklearn.SVM中,SVC表示用SVM完成分类任务,SVR表示用SVM完成回归任务,这里我们选用SVC。此外,它的参数和我们上面的公式在表达上有细微的区别。对于RBF核函数,其参数为
# 从sklearn.svm中导入SVM分类器from sklearn.svm import SVC# 定义SVM模型,包括定义使用的核函数与参数信息model = SVC(kernel='rbf', gamma=50, tol=1e-6)model.fit(x, y)# 绘制结果fig = plt.figure(figsize=(6,6))G = np.linspace(-1.5, 1.5, 100)G = np.meshgrid(G, G)X = np.array([G[0].flatten(), G[1].flatten()]).T # 转换为每行一个向量的形式Y = model.predict(X)Y = Y.reshape(G[0].shape)plt.contourf(G[0], G[1], Y, cmap=cmap, alpha=0.5)# 绘制原数据集的点plt.scatter(x[y == -1, 0], x[y == -1, 1], color='red', label='y=-1')plt.scatter(x[y == 1, 0], x[y == 1, 1], marker='x', color='blue', label='y=1')plt.xlabel(r'$x_1$')plt.ylabel(r'$x_2$')plt.legend()plt.show()
11.6 本章小结
本章介绍了支持向量机的原理及其求解算法SMO。由于SVM属于非参数化模型,其模型中的参数与数据集的规模相同,求解较为复杂,但SMO算法大大降低了求解的难度。并且在求解完成后,我们只需要保留支持向量,就可以继续利用模型完成后续的预测任务,其时间和空间复杂度都下降很多。对于非线性分布的数据,我们可以通过引入非线性的核函数使SVM完成分类任务,达到和神经网络中激活函数类似的效果。
不同的核函数适用的场景有所不同,其中最常用的是RBF核函数。但是它对参数
习题
以下关于SVM的说法不正确的是: A. SVM的目标是寻找一个使最小几何间隔达到最大值的分割超平面。 B. 分割超平面不会随
以下关于核函数的说法不正确的是: A. 核函数的数值大小反映了两个变量之间的相似度高低。 B. SVM只着眼于内积计算,因此训练时可以使用核函数来代替特征映射
在逻辑斯谛回归中,我们也用解析方式求出了模型参数,但是其中涉及复杂度很高的矩阵乘法和矩阵求逆。为什么支持向量机的解析结果中不包含这类复杂运算?(提示:逻辑斯谛回归和支持向量机分别考虑了样本到分隔平面的什么间隔?)
对于同一个数据集,逻辑斯谛回归和支持向量机给出的分隔平面一样吗?用本章的
linear.csv数据集验证你的想法。试着给数据集中手动添加一些新的样本点,或者更改已有样本点的分类。两种算法给出的分隔平面有什么变化?思考RBF核函数对应的
试基于本章代码,标记出双螺旋数据上使用RBF核函数的SVM模型的支持向量,并讨论这些数据点成为支持向量的原因。
试通过参数量与数据集大小的关系、参数更新方式等视角,分析和体会SVM模型的原问题对应参数化模型,而对偶问题对应非参数化模型。
拓展阅读:SVM对偶问题的推导
对一般形式的带约束的凸优化问题
定义其拉格朗日函数(Lagrangian function)为:
其中
并且定义参数
于是,最开始带约束的优化问题等价于对原问题的无约束优化 :
记该问题的最优值为
至此,我们只是通过拉格朗日函数对原问题进行了等价变形,并没有降低问题求解的难度。为了真正解决该优化问题,我们考虑另一个稍微有些区别的函数
将上面优化问题中计算
记其最优值为
- 最优值
以及卡鲁什-库恩-塔克条件(Karush-Kuhn-Tucker conditions),简称KKT条件:
- 稳定性:
- 原问题满足性:
- 对偶问题满足性:
- 互补松弛性:
反过来,如果某一组
根据上面的讨论,如果一个凸优化问题满足KKT条件,且其对偶问题比原问题更容易解决,那么我们可以通过求对偶问题的解来得到原问题的解。对线性版本的支持向量机的优化问题
来说,
为了求其最小值
我们把
于是,对偶优化问题的形式为:
而引入松弛变量
其中