- 12.2 ID3决策树与C4.5决策树
- 12.3 CART决策树
- 12.3 动手实现C4.5决策树
- 12.3.1 数据集处理
- 12.3.2 C4.5的实现
- 12.4 Sklearn中的决策树
- 12.5 本章小结
- 习题
- 参考文献
第 12 章 决策树
本章开始,我们将介绍机器学习中与神经网络并行的另一大类非参数化模型——决策树(decision tree)模型及其变种。决策树模型简称树模型,顾名思义,它采用了和树类似的结构。图12-1展示了现实中的树与计算机中的树的异同。现实中的树是根在下、从下向上生长的,计算机中的树却是根在上、从上向下生长的。但是,两者都有根、枝干的分叉与叶子。在计算机的树中,最上面的节点称为根节点,最下面没有分叉的节点称为叶节点。其中,根节点和内部节点都有一些边指向其他节点,这些被指向的节点就称为它的子节点。叶节点是树的最末端,没有指向其他节点的边。而除了根节点之外,每个内部节点和叶节点都有唯一的节点指向它,该节点称为其父节点。
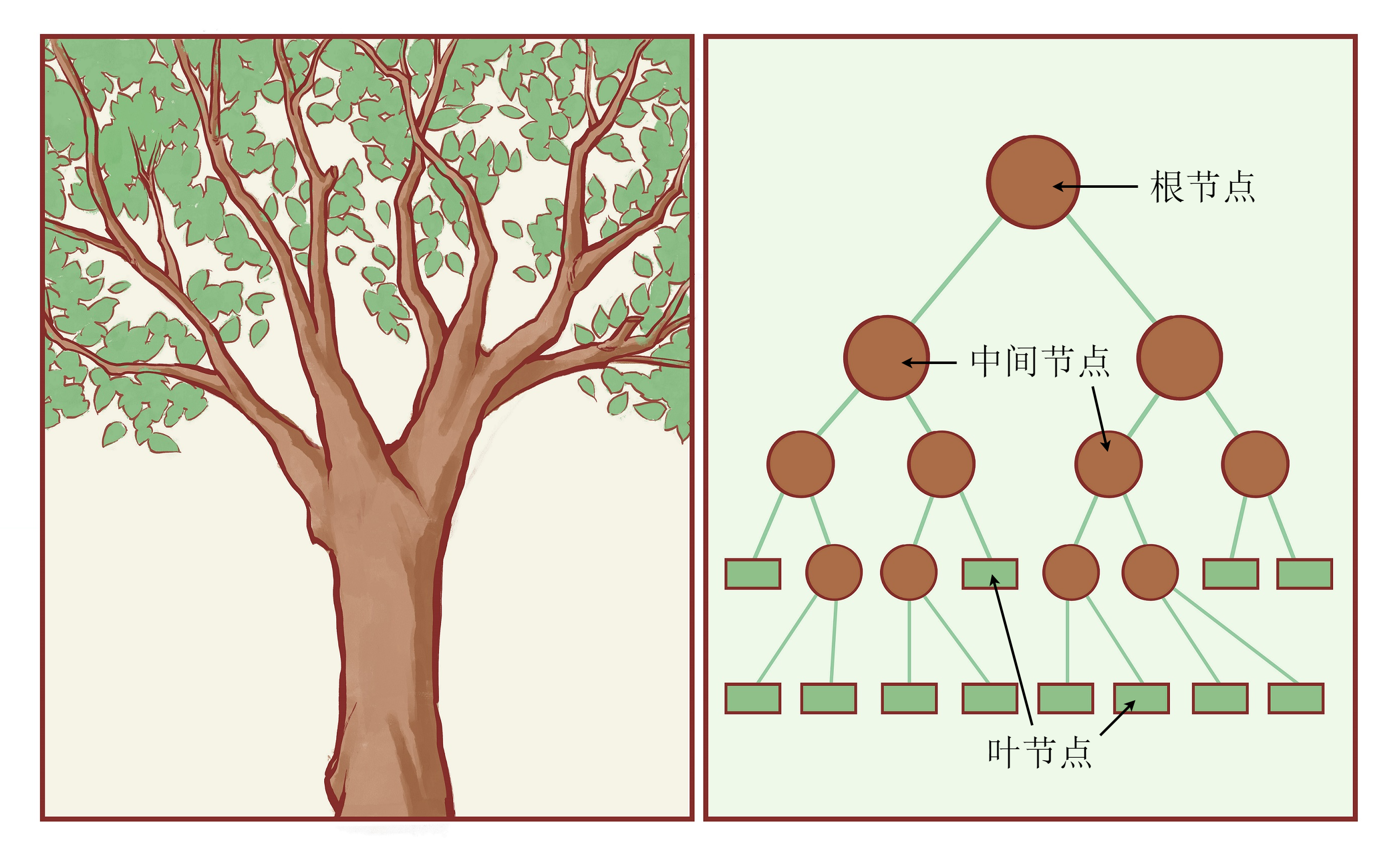
如果读者对数据结构中的树有一些了解的话,应该很容易理解其构造。不过决策树并不需要用到数据结构的相关知识,我们可以简单地将这棵树看作一张流程图。在一棵决策树中,根节点和内部节点的作用是相同的,后面我们将其统称为内部节点。设输入样本为
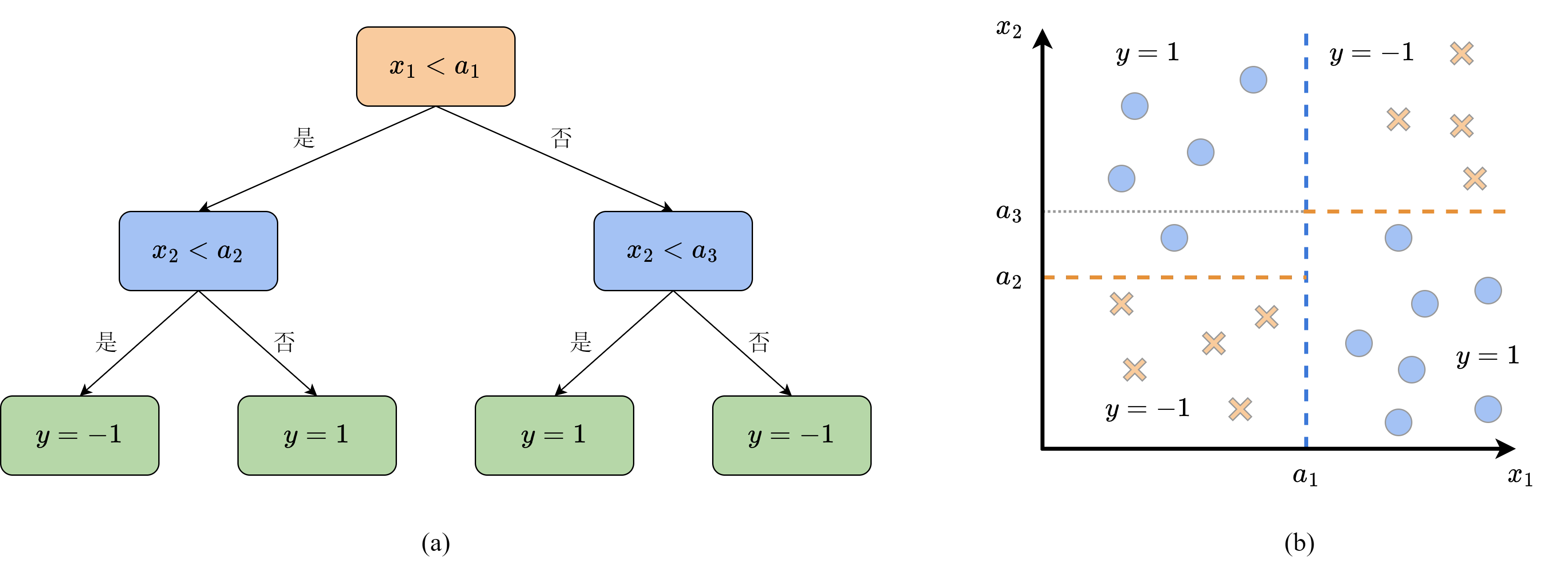
决策树由于其分支离散的特性,通常用来完成分类任务。在直角坐标系中,其分类的边界是与坐标轴平行的直线。图12-2展示了一棵简单的二分类决策树和其对应的分类边界,其输入是平面上的点
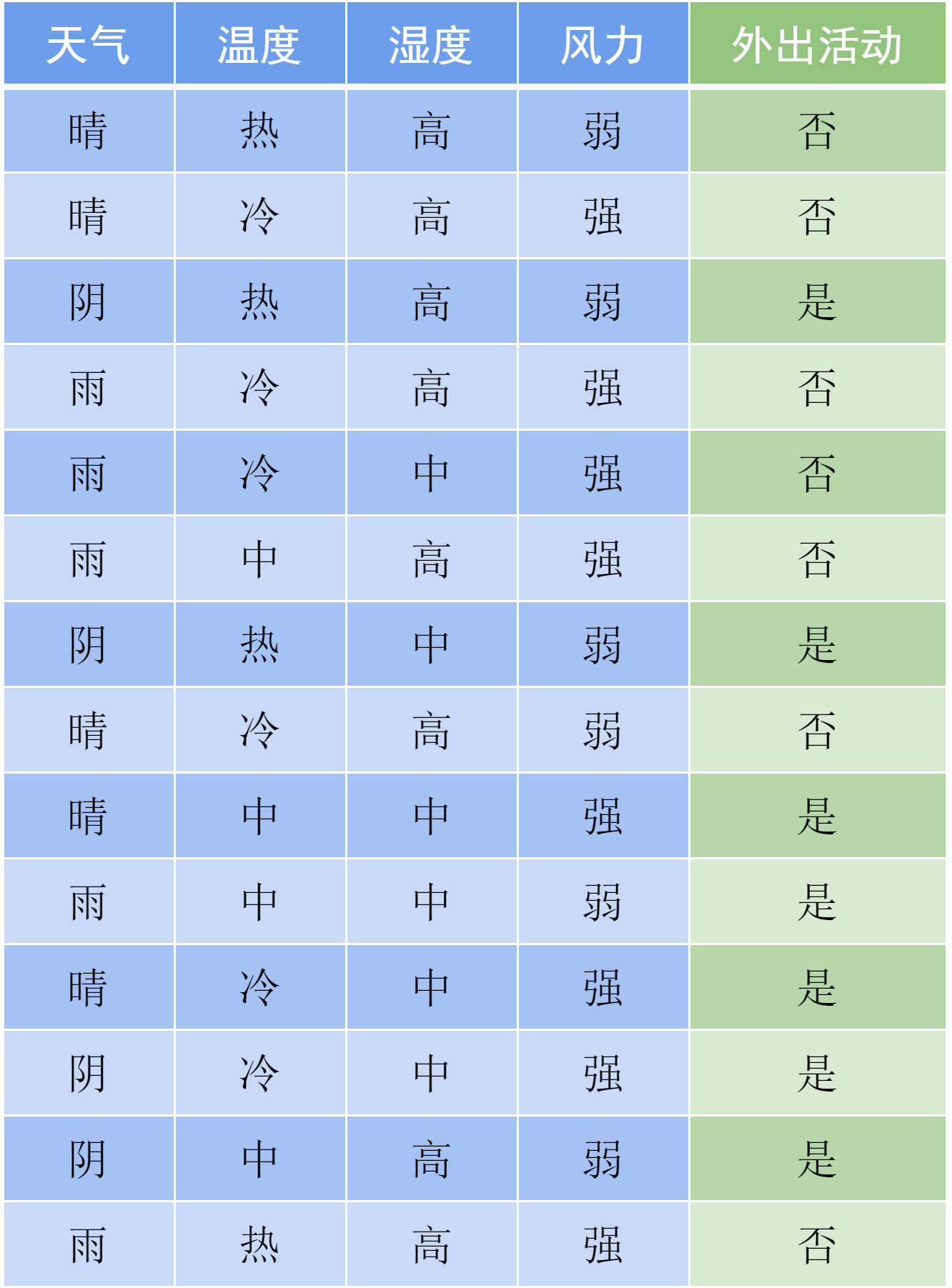
那么,该如何为每个内部节点选择合适的表达式呢?我们的目标是使最终构造的决策树复杂度尽可能低,换句话说,判断一个样本的类别需要的期望次数尽可能少。我们来看下面的例子,表12-1是过去一段时间内小明是否外出活动和天气条件的关系。天气条件共有4个特征,其中天气和温度分别有3种取值,湿度和风力分别有2种取值。
表 12-1 外出活动与天气条件的关系表
我们来考虑从该表格中的数据构造决策树时,如何选择根节点上用来分类的特征。直观上,为了使整体复杂度最低,我们希望每一次分类都可以把不同类的样本尽可能分开,因此应当首先将有3种取值的特征放在根节点上。我们尝试用天气或温度作为根节点对数据进行一次分类,得到的两种决策树如图12-3所示。图中的每个圆点对应表格中的一个样本,红色表示没有外出活动,绿色表示外出活动。
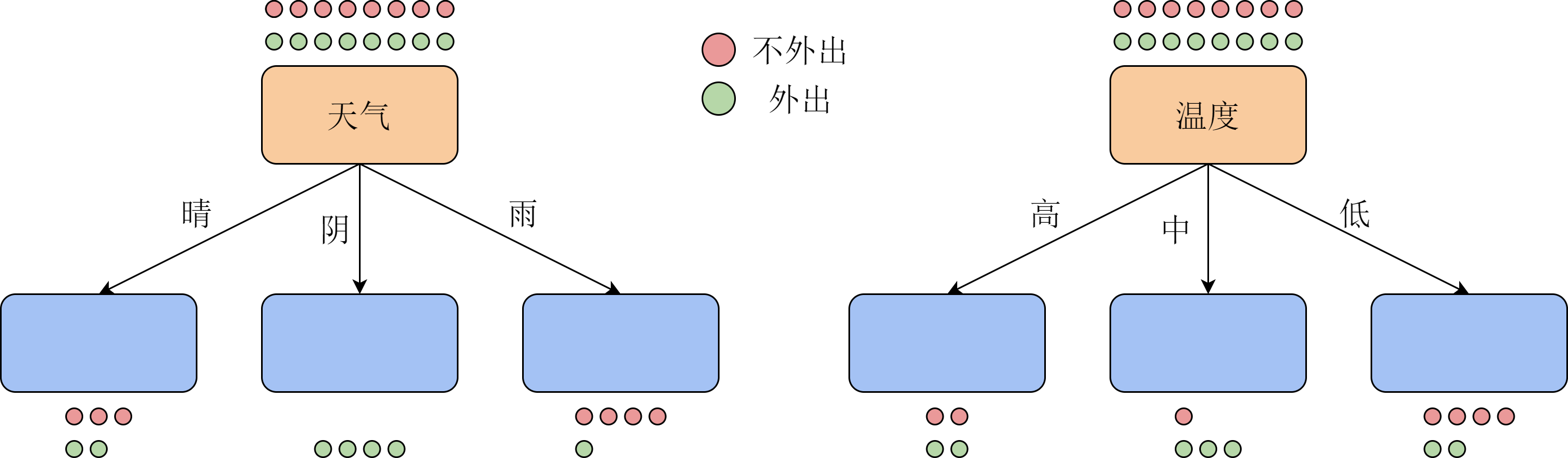
两种分类方式得到的一次分类结果并不相同。可以看出,以天气作为特征,一次就可以将所有阴天的情况分好,接下来再分别考虑晴天和雨天;而以温度为特征,3种取值都需要进一步选择其他特征进行分类。换句话说,当我们知道了样本中的天气时,所获得的信息量比知道样本中的温度要大。而一个数据集总体的信息量是恒定的,因此,我们在每一步都应当选择能获得更多信息的特征作为分类标准。
在第6章逻辑斯谛回归中,我们已经介绍了信息量与信息熵的概念,这里再直接从随机变量的角度回顾一下。设离散随机变量
如果将随机变量
我们通常用概率分布的熵的变化来作为信息的度量。当我们为一个分布引入额外信息时,其不确定度会减小,所以熵会降低。为此,我们引入条件熵的概念。在给定
如果随机变量
在决策树中,记数据集中样本的类别是
- 原始数据:共有14个样本,未外出活动
的样本与外出活动 的样本各占一半,从而:
用天气分类:记晴天为
,阴天为 ,雨天为 。 - 晴天样本5个,其中外出2个,未外出3个,得
- 阴天样本4个,其中外出4个,未外出0个,得
- 雨天样本5个,其中外出1个,未外出4个,得
- 条件熵
- 获得信息
用温度分类:记高温为
,适中为 ,低温为 。类似可得:
通过计算可以直观地看出,用天气进行分类所获得的信息大于用温度分类所获得的信息。但是,引入某个特征
其中,
式中,
- 用天气分类:统计数量得
,于是:
- 用温度分类:统计数量得
,于是:
比较信息增益率的大小,我们发现用天气作为分类特征确实是最优的选择。读者可以自行验算,取湿度或风力作为分类特征的信息增益率都比用天气分类要小。综上所述,我们可以通过在每个节点上选取信息增益率最大的分类特征来构建决策树,从而使其整体复杂度较低。
12.2 ID3决策树与C4.5决策树
由Ross Quinlan在1986年提出的ID3(iterative dichotomiser 3)算法
由于ID3算法倾向于无限精细划分,它存在两个较为严重的问题。第一个问题是,如果用于划分的特征本身就较为复杂,就会出现上文提到的复杂度转移现象。一方面,继续分类的复杂度只是转移到了分支选择上;另一方面,这样的精细分类极有可能只对当前的训练集适用,容易出现过拟合现象。因此,我们可以将选取特征的标准由信息增益
第二个问题是,ID3算法直到将所有数据分类完成才会停止,如果数据集中包含较多相似的数据,ID3算法构造的决策树就会出现非常长的分支,大大增加算法的复杂度。我们需要在分类准确率和决策树的复杂度之间寻找平衡。例如服装厂生产的衣服尺寸,以身高来说,如果只生产尺寸为170cm的衣服显然无法满足需求;而如果为每个不同身高的人都生产相应身高的衣服,成本显然又太高。因此,服装厂可能会将身高以
该式可以用来衡量该叶节点分类的精度。利用这一函数,我们将代价函数
其中,
12.3 CART决策树
在前两节中,我们介绍的ID3决策树和其改进算法C4.5决策树都只能解决分类问题。决策树中每个节点的分叉在将整个空间不断划分,最后得到的每个叶子节点对应空间中的一块区域,而模型就认为该区域中的样本都属于同一类别。对于回归问题来说,这一思路同样适用。我们可以将同一叶节点内样本标签值的平均来作为模型对该区域的预测。但是,ID3和C4.5的节点划分是以离散随机变量的熵为基础的,并不能很好衡量回归问题下划分带来的收益。因此,分类和回归树(classification and regression tree,CART)
假设样本
作为回归问题,我们可以用最经典的MSE损失当作优化目标:
容易计算出,当模型在区域上的预测值
注意CART回归树不仅需要处理离散特征,还需要处理连续取值的特征。因此,我们在节点划分时不仅需要找到最优特征,还需要判断最优的划分阈值假设我们选择了特征
其中
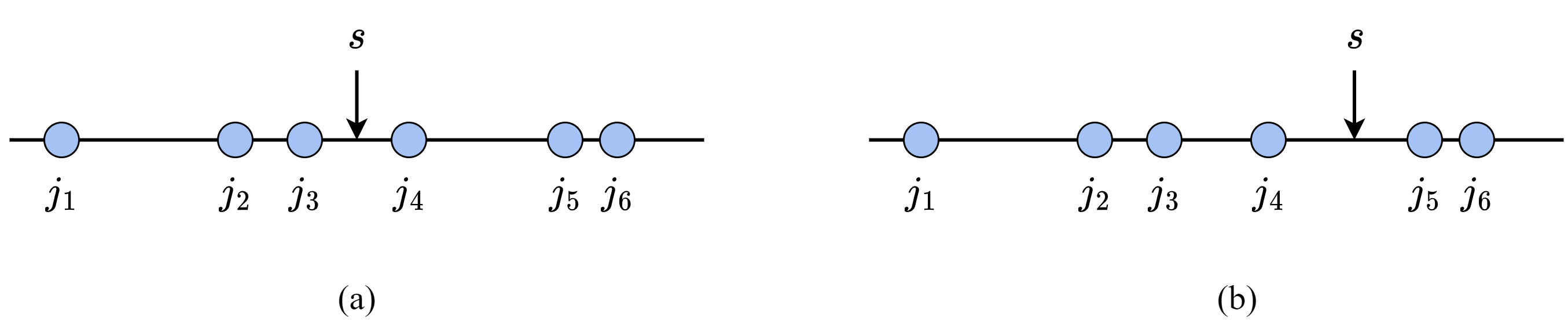
其中,
可以看出,为了快速计算
这样,无论
除了回归树之外,CART模型同样可以用来构建分类树,只不过它使用的节点划分指标从信息增益率变为了计算更简单的基尼不纯度(Gini impurity)。设
上式是关于
在实际应用时,设分类问题共有
与分类树类似,假设我们选择的特征
上式是对于连续特征而言的。在实际问题中,常常还有离散有限取值的特征,例如图 12-3 所示。这时,设选择的取值为
最后,我们把两个子集的基尼不纯度按子集大小为比例相加,作为以特征
在每次划分时,我们选择使基尼不纯度最小的
12.3 动手实现C4.5决策树
本节我们来动手实现ID3决策树的改进版本C4.5决策树。虽然C4.5决策树只能解决分类问题,但是在实践中,我们仍然可能在分类问题中遇到连续取值的特征。在下面的数据处理过程中,我们会介绍一种在决策树中常用的把连续特征离散化的方法,该方法在C4.5和CART决策树中都有使用。由于CART分类树与C4.5的整体结构没有太大差别,只是划分标准不同,我们在这里只实现C4.5决策树,把CART分类树的实现留作习题供读者练习。
12.3.1 数据集处理
本章用到的数据集是泰坦尼克号的生存预测数据集,它包含了许多泰坦尼克号上的乘客的特征信息,以及该乘客最后是否生还。表12-2按顺序列出了每一行包含的信息及其格式。
表 12-2 泰坦尼克生存数据集中的样本特征
| 列编号 | 特征名称 | 含义 | 取值 |
|---|---|---|---|
| 0 | 'PassengerId' | 编号,从1开始 | 整数 |
| 1 | 'Survived' | 是否生还,1代表生还,0代表遇难 | 0、1 |
| 2 | 'Pclass' | 舱位等级 | 0、1、2 |
| 3 | 'Name' | 姓名 | 字符串 |
| 4 | 'Sex' | 性别 | 'male'、'female' |
| 5 | 'Age' | 年龄 | 浮点数 |
| 6 | 'SibSp' | 登船的兄弟姐妹数量 | 整数 |
| 7 | 'Parch' | 登船的父母和子女数量 | 整数 |
| 8 | 'Ticket' | 船票编号 | 字符串 |
| 9 | 'Fare' | 船票价格 | 浮点数 |
| 10 | 'Cabin' | 所在船舱编号 | 字符串 |
| 11 | 'Embarked' | 登船港口,C代表瑟堡,S代表南安普敦,Q代表昆斯敦) | 'C'、'S'、'Q' |
其中,部分乘客的信息中部分字段有可能缺失。对这些特征进行一些初步的分析可以发现,乘客的编号、姓名、船票编号都是唯一的,船舱编号也较为零散,对建立模型帮助较小。因此,我们在预处理时直接将这四个字段删去。原始的数据集中包含训练集和测试集,但测试集中不包含乘客是否生还的标签,我们无法验证决策树的分类精度。所以本章中将原本的训练集按8:2的比例划分为训练集和测试集,以此来代替原本的测试集。
由于数据集的不同字段类型不同,直接用NumPy读取和处理不太方便,我们采用另一个专门为数据分析和处理而设计的工具库Pandas来完成数据预处理工作,它可以自动识别字段的数据类型,并将不同字段用不同的数据类型存储。由Pandas读入的数据存储在pandas.DataFrame实例中,我们可以将其看作是扩展的numpy.ndarray,其许多操作都和ndarray相同。
import numpy as npimport matplotlib.pyplot as pltimport pandas as pd# 读取数据data = pd.read_csv('titanic/train.csv')# 查看数据集信息和前5行具体内容,其中NaN代表数据缺失print(data.info())print(data[:5])# 删去编号、姓名、船票编号3列data.drop(columns=['PassengerId', 'Name', 'Ticket'], inplace=True)
<class 'pandas.core.frame.DataFrame'>RangeIndex: 891 entries, 0 to 890Data columns (total 12 columns):# Column Non-Null Count Dtype--- ------ -------------- -----0 PassengerId 891 non-null int641 Survived 891 non-null int642 Pclass 891 non-null int643 Name 891 non-null object4 Sex 891 non-null object5 Age 714 non-null float646 SibSp 891 non-null int647 Parch 891 non-null int648 Ticket 891 non-null object9 Fare 891 non-null float6410 Cabin 204 non-null object11 Embarked 889 non-null objectdtypes: float64(2), int64(5), object(5)memory usage: 83.7+ KBNonePassengerId Survived Pclass \0 1 0 31 2 1 12 3 1 33 4 1 14 5 0 3Name Sex Age SibSp \0 Braund, Mr. Owen Harris male 22.0 11 Cumings, Mrs. John Bradley (Florence Briggs Th... female 38.0 12 Heikkinen, Miss. Laina female 26.0 03 Futrelle, Mrs. Jacques Heath (Lily May Peel) female 35.0 14 Allen, Mr. William Henry male 35.0 0Parch Ticket Fare Cabin Embarked0 0 A/5 21171 7.2500 NaN S1 0 PC 17599 71.2833 C85 C2 0 STON/O2. 3101282 7.9250 NaN S3 0 113803 53.1000 C123 S4 0 373450 8.0500 NaN S
在上面的算法介绍中,我们只考虑了特征取离散值的情况。在实践中,还有许多特征的取值是连续的,例如本数据集中的年龄和船票价格两项。对于这样的特征,我们可以根据数据的范围划出几个分类点,按照取值与分类点的大小关系进行分类。假设有
feat_ranges = {}cont_feat = ['Age', 'Fare'] # 连续特征bins = 10 # 分类点数for feat in cont_feat:# 数据集中存在缺省值nan,需要用np.nanmin和np.nanmaxmin_val = np.nanmin(data[feat])max_val = np.nanmax(data[feat])feat_ranges[feat] = np.linspace(min_val, max_val, bins).tolist()print(feat, ':') # 查看分类点for spt in feat_ranges[feat]:print(f'{spt:.4f}')
Age :0.42009.262218.104426.946735.788944.631153.473362.315671.157880.0000Fare :0.000056.9255113.8509170.7764227.7019284.6273341.5528398.4783455.4037512.3292
对于只有有限个取值的离散特征,我们将其转化为整数。
# 只有有限取值的离散特征cat_feat = ['Sex', 'Pclass', 'SibSp', 'Parch', 'Cabin', 'Embarked']for feat in cat_feat:data[feat] = data[feat].astype('category') # 数据格式转为分类格式print(f'{feat}:{data[feat].cat.categories}') # 查看类别data[feat] = data[feat].cat.codes.to_list() # 将类别按顺序转换为整数ranges = list(set(data[feat]))ranges.sort()feat_ranges[feat] = ranges
Sex:Index(['female', 'male'], dtype='object')Pclass:Int64Index([1, 2, 3], dtype='int64')SibSp:Int64Index([0, 1, 2, 3, 4, 5, 8], dtype='int64')Parch:Int64Index([0, 1, 2, 3, 4, 5, 6], dtype='int64')Cabin:Index(['A10', 'A14', 'A16', 'A19', 'A20', 'A23', 'A24', 'A26', 'A31', 'A32',...'E8', 'F E69', 'F G63', 'F G73', 'F2', 'F33', 'F38', 'F4', 'G6', 'T'],dtype='object', length=147)Embarked:Index(['C', 'Q', 'S'], dtype='object')
由于数据中存在缺省值,我们将所有缺省值填充为-1,并为所有特征的分类点添加最小值-1。这一做法是处理缺省值的最简单的方式。如果要更合理地填充缺省值,我们可以通过数据集中其他相似的样本对缺省值进行推断,感兴趣的读者可以自行查阅相关资料。此外,我们再统计标签的可能取值,在计算熵时使用。
# 将所有缺省值替换为-1data.fillna(-1, inplace=True)for feat in feat_ranges.keys():feat_ranges[feat] = [-1] + feat_ranges[feat]
最后,我们按8:2的比例划分训练集与测试集,并将数据从pandas.DataFrame转换为更通用的numpy.ndarray,完成整个数据处理过程。
# 划分训练集与测试集np.random.seed(0)feat_names = data.columns[1:]label_name = data.columns[0]# 重排下标之后,按新的下标索引数据data = data.reindex(np.random.permutation(data.index))ratio = 0.8split = int(ratio * len(data))train_x = data[:split].drop(columns=['Survived']).to_numpy()train_y = data['Survived'][:split].to_numpy()test_x = data[split:].drop(columns=['Survived']).to_numpy()test_y = data['Survived'][split:].to_numpy()print('训练集大小:', len(train_x))print('测试集大小:', len(test_x))print('特征数:', train_x.shape[1])
训练集大小: 712测试集大小: 179特征数: 8
12.3.2 C4.5的实现
下面我们实现C4.5算法的主体部分。在上面的算法介绍中,我们在按特征划分节点时,为特征的每种可能取值都分裂出一个新节点。然而在实践中,为了控制算法的复杂度,提升最后的准确率,我们通常采用二分类法。对于数据的某个特征
对于树模型来说,最基础的单元就是树上的节点,所以我们先来定义节点类。节点中存储分类特征、分类点的值和子节点列表。
class Node:def __init__(self):# 内部节点的feat表示用来分类的特征编号,其数字与数据中的顺序对应# 叶节点的feat表示该节点对应的分类结果self.feat = None# 分类值列表,表示按照其中的值向子节点分类self.split = None# 子节点列表,叶节点的child为空self.child = []
考虑到代码整体的结构和可读性,我们将决策树也定义成类,将具体的实现细节以注释的形式标注在类中。对照我们前面的讲解,该类应当能计算熵、信息增益、信息增益率等值,可以从根节点开始用C4.5算法生成决策树,还可以用建立好的决策树预测新样本的分类。下面,我们就按照这一思路,依次实现决策树的各个部分。
class DecisionTree:def __init__(self, X, Y, feat_ranges, lbd):self.root = Node()self.X = Xself.Y = Yself.feat_ranges = feat_ranges # 特征取值范围self.lbd = lbd # 正则化系数self.eps = 1e-8 # 防止数学错误log(0)和除以0self.T = 0 # 记录叶节点个数self.ID3(self.root, self.X, self.Y)# 工具函数,计算 a * log adef aloga(self, a):return a * np.log2(a + self.eps)# 计算某个子数据集的熵def entropy(self, Y):cnt = np.unique(Y, return_counts=True)[1] # 统计每个类别出现的次数N = len(Y)ent = -np.sum([self.aloga(Ni / N) for Ni in cnt])return ent# 计算用feat <= val划分数据集的信息增益def info_gain(self, X, Y, feat, val):# 划分前的熵N = len(Y)if N == 0:return 0HX = self.entropy(Y)HXY = 0 # H(X|Y)# 分别计算H(X|X_F<=val)和H(X|X_F>val)Y_l = Y[X[:, feat] <= val]HXY += len(Y_l) / len(Y) * self.entropy(Y_l)Y_r = Y[X[:, feat] > val]HXY += len(Y_r) / len(Y) * self.entropy(Y_r)return HX - HXY# 计算特征feat <= val本身的复杂度H_Y(X)def entropy_YX(self, X, Y, feat, val):HYX = 0N = len(Y)if N == 0:return 0Y_l = Y[X[:, feat] <= val]HYX += -self.aloga(len(Y_l) / N)Y_r = Y[X[:, feat] > val]HYX += -self.aloga(len(Y_r) / N)return HYX# 计算用feat <= val划分数据集的信息增益率def info_gain_ratio(self, X, Y, feat, val):IG = self.info_gain(X, Y, feat, val)HYX = self.entropy_YX(X, Y, feat, val)return IG / HYX# 用ID3算法递归分裂节点,构造决策树def ID3(self, node, X, Y):# 判断是否已经分类完成if len(np.unique(Y)) == 1:node.feat = Y[0]self.T += 1return# 寻找最优分类特征和分类点best_IGR = 0best_feat = Nonebest_val = Nonefor feat in range(len(feat_names)):for val in self.feat_ranges[feat_names[feat]]:IGR = self.info_gain_ratio(X, Y, feat, val)if IGR > best_IGR:best_IGR = IGRbest_feat = featbest_val = val# 计算用best_feat <= best_val分类带来的代价函数变化# 由于分裂叶节点只涉及该局部,我们只需要计算分裂前后该节点的代价函数# 当前代价cur_cost = len(Y) * self.entropy(Y) + self.lbd# 分裂后的代价,按best_feat的取值分类统计# 如果best_feat为None,说明最优的信息增益率为0,# 再分类也无法增加信息了,因此将new_cost设置为无穷大if best_feat is None:new_cost = np.infelse:new_cost = 0X_feat = X[:, best_feat]# 获取划分后的两部分,计算新的熵new_Y_l = Y[X_feat <= best_val]new_cost += len(new_Y_l) * self.entropy(new_Y_l)new_Y_r = Y[X_feat > best_val]new_cost += len(new_Y_r) * self.entropy(new_Y_r)# 分裂后会有两个叶节点new_cost += 2 * self.lbdif new_cost <= cur_cost:# 如果分裂后代价更小,那么执行分裂node.feat = best_featnode.split = best_vall_child = Node()l_X = X[X_feat <= best_val]l_Y = Y[X_feat <= best_val]self.ID3(l_child, l_X, l_Y)r_child = Node()r_X = X[X_feat > best_val]r_Y = Y[X_feat > best_val]self.ID3(r_child, r_X, r_Y)node.child = [l_child, r_child]else:# 否则将当前节点上最多的类别作为该节点的类别vals, cnt = np.unique(Y, return_counts=True)node.feat = vals[np.argmax(cnt)]self.T += 1# 预测新样本的分类def predict(self, x):node = self.root# 从根节点开始向下寻找,到叶节点结束while node.split is not None:# 判断x应该处于哪个子节点if x[node.feat] <= node.split:node = node.child[0]else:node = node.child[1]# 到达叶节点,返回类别return node.feat# 计算在样本X,标签Y上的准确率def accuracy(self, X, Y):correct = 0for x, y in zip(X, Y):pred = self.predict(x)if pred == y:correct += 1return correct / len(Y)
最后,我们用训练集构造决策树,并在测试集上检测决策树的分类效果。读者可以通过调节正则化系数
DT = DecisionTree(train_x, train_y, feat_ranges, lbd=1.0)print('叶节点数量:', DT.T)# 计算在训练集和测试集上的准确率print('训练集准确率:', DT.accuracy(train_x, train_y))print('测试集准确率:', DT.accuracy(test_x, test_y))
叶节点数量: 23训练集准确率: 0.8300561797752809测试集准确率: 0.7262569832402235
12.4 Sklearn中的决策树
Sklearn中也提供了决策树工具,包括分类型决策树DecisionTreeClassifier和回归型决策树DecisionTreeRegressor,这两种决策树都内置了不同的节点划分标准,可以通过参数来调整。下面,我们直接使用分类型决策树在我们处理好的数据集上进行训练。由于sklearn中进行了大量优化,其最终的预测精度要比本章手动实现的高一些。但是,sklearn的决策树也含有大量的超参数,想要达到最优的结果往往需要复杂的调参过程。下面我们只展示了max_depth一个超参数,它表示决策树的最大深度,即从根到任意一个叶节点的最长路径的长度。该参数与我们的正则化类似,也能起到控制决策树复杂度的效果。
from sklearn import tree# criterion表示分类依据,max_depth表示树的最大深度# entropy生成的是C4.5分类树c45 = tree.DecisionTreeClassifier(criterion='entropy', max_depth=6)c45.fit(train_x, train_y)# gini生成的是CART分类树cart = tree.DecisionTreeClassifier(criterion='gini', max_depth=6)cart.fit(train_x, train_y)c45_train_pred = c45.predict(train_x)c45_test_pred = c45.predict(test_x)cart_train_pred = cart.predict(train_x)cart_test_pred = cart.predict(test_x)print(f'训练集准确率:C4.5:{np.mean(c45_train_pred == train_y)},' \f'CART:{np.mean(cart_train_pred == train_y)}')print(f'测试集准确率:C4.5:{np.mean(c45_test_pred == test_y)},' \f'CART:{np.mean(cart_test_pred == test_y)}')
训练集准确率:C4.5:0.8834269662921348,CART:0.8848314606741573测试集准确率:C4.5:0.7262569832402235,CART:0.7932960893854749
PyDotPlus库提供了将sklearn生成的决策树可视化的工具。我们可以将训练得到的决策树做可视化,观察在每个节点上决策树选择了哪个特征进行分类。由于生成的图像较宽,无法完全清晰展示,我们将决策树的左右子树分开放在图12-5中。读者可以自行运行代码,查看完整的生成图像。
!pip install pydotplusfrom six import StringIOimport pydotplusdot_data = StringIO()tree.export_graphviz( # 导出sklearn的决策树的可视化数据c45,out_file=dot_data,feature_names=feat_names,class_names=['non-survival', 'survival'],filled=True,rounded=True,impurity=False)# 用pydotplus生成图像graph = pydotplus.graph_from_dot_data(dot_data.getvalue().replace('\n', ''))graph.write_png('tree.png')
True
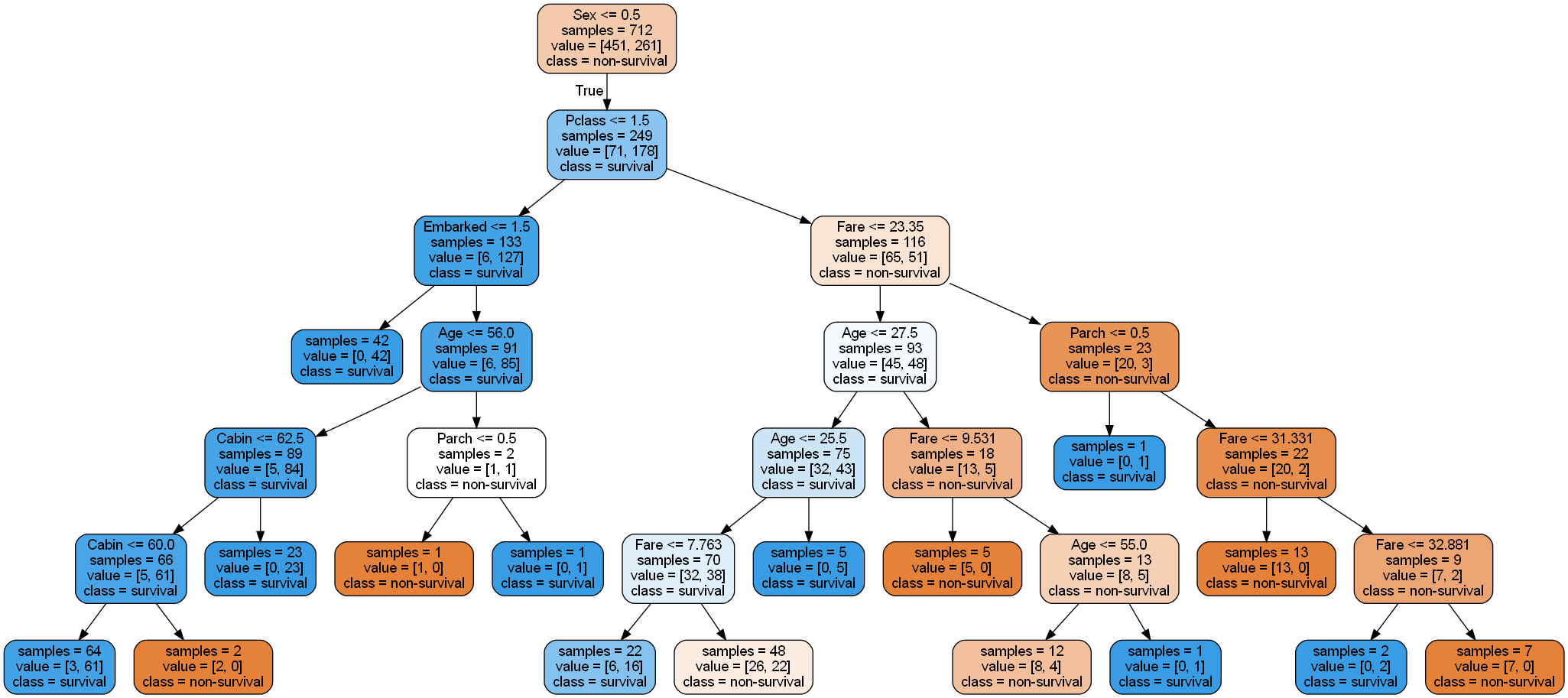
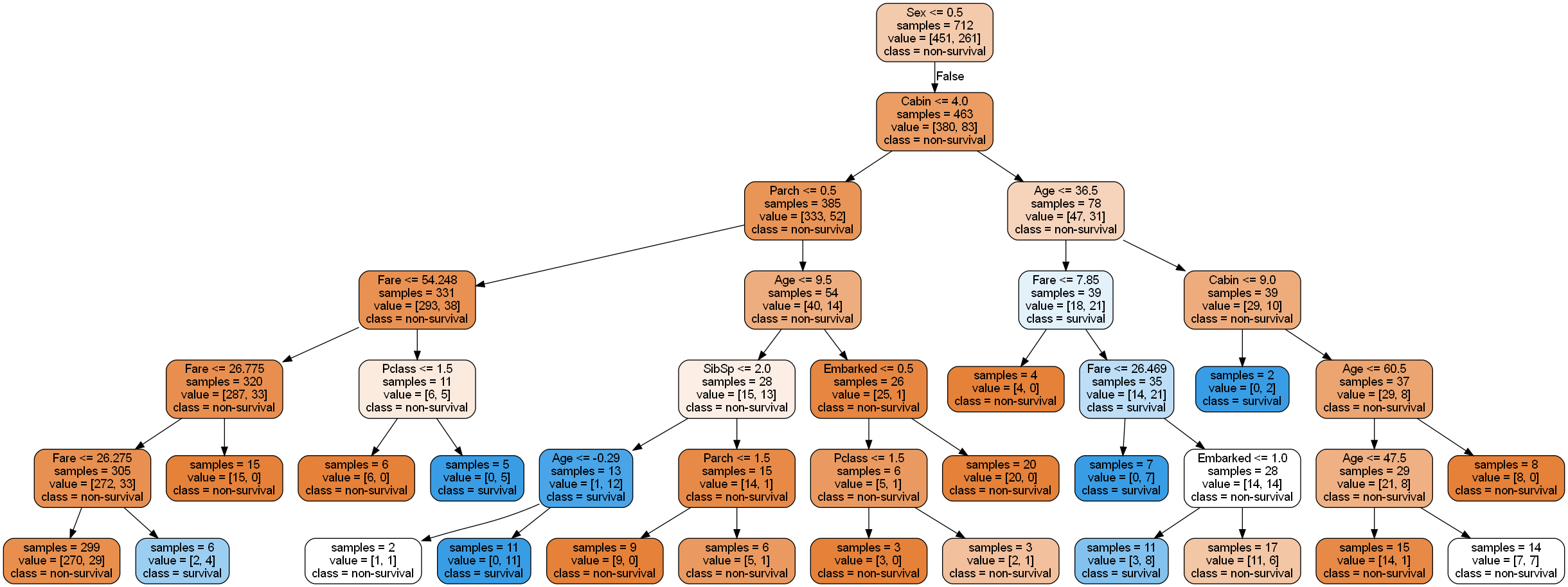
图 12-5 算法最终生成的决策树示意图
12.5 本章小结
本章介绍了决策树模型的基本概念和最基础的决策树生成算法ID3算法。决策树是继KNN之后,本书介绍的第二个非参数化模型。决策树的生成过程就是直接在树模型空间中构建新的分裂节点,不断选择特征和分裂值,使整体的熵降低的过程。关于特征选择的标准,ID3算法采用简单的信息增益;其改进版C4.5考虑了特征本身的复杂度,选择信息增益率来代替信息增益。此外,CART算法使用基尼不纯度作为选择标准,计算较为简单;并且它还可以用误差平方和作为选择标准来完成回归任务,在连续特征的数据集上有更好的效果。由于决策树本身倾向于将数据完全精确分类,非常容易出现过拟合现象,因此我们需要用代价函数、最大深度等约束限制其生长。像这样,在决策树构造时就避免其过度生长的方法称为前剪枝(pre-pruning)。也有一些方法在决策树生成后,通过遍历决策树判断节点分裂的价值,从而删除部分叶节点,称为后剪枝(post-pruning)。决策树由于其便于可视化、可解释性强,在一段时间内是非常流行的算法,其中C4.5算法及其变种曾在2008年被评为“数据挖掘十大算法”之首
习题
以下关于决策树的说法错误的是: A. 决策树选择具有更强分类能力的特征进行分裂。 B. 决策树只能处理分类问题,无法处理连续的回归问题。 C. 决策树可以解决非线性可分的分类问题。 D. 决策树的预测结果分布在叶子节点上。
以下关于ID3算法的说法错误的是: A. 由ID3算法构建的决策树,一个特征不会在同一条路径中出现两次。 B. 作为非参数化模型,ID3算法不会出现过拟合。 C. 在节点分裂出来的树枝数目取决于分类特征可能取值的数量。 D. 信息增益率为信息增益与熵之间的比值,可以排除特征本身复杂度的影响。
设
和 是相互独立的随机变量,证明:
其中
在12.1节的例子中,计算用湿度为标准进行一次分类的信息增益和信息增益率。
在本章C4.5决策树代码的基础上实现CART分类树。
尝试将决策树应用到第11章支持向量机中用到的linear.csv和spiral.csv分类数据集上。先猜想一下分类效果与支持向量机相比如何,再用实验验证你的猜想。注意,需要先对连续特征离散化。
假设在一个二维数据的二分类任务中,最优分类边界是
,但是决策树模型只能沿着坐标轴的方向去切分二维数据空间,这样耗费很多分裂节点也无法取得很好的分类性能,试思考在此类情形下应该如何应对。
参考文献
[1] ID3算法论文:Quinlan J R. Induction of decision trees[J]. Machine learning, 1986, 1: 81-106.
[2] C4.5算法论文:Quinlan J R. C4. 5: programs for machine learning[M]. Elsevier, 2014.
[3] CART算法论文:Breiman L. Classification and regression trees[M]. Routledge, 2017.
[4] 数据挖掘十大算法:Wu X, Kumar V, Ross Quinlan J, et al. Top 10 algorithms in data mining[J]. Knowledge and information systems, 2008, 14: 1-37.