- 9.1 卷积
- 9.2 神经网络中的卷积
- 9.3 用卷积神经网络完成图像分类任务
- 9.4 用预训练的卷积神经网络完成色彩风格迁移
- 9.4.1 VGG 网络
- 9.4.2 内容与风格表示
- 9.5 本章小结
- 习题
- 参考文献
- 拓展阅读:数据增强
第 9 章 卷积神经网络
本章继续讲解基于神经网络的模型。在MLP中,层与层的神经元之间两两连接,模拟了线性变换
9.1 卷积
卷积(convolution)是一种数学运算。对于两个函数
如果函数是离散的,假设其定义在整数集合
这两个式子理解起来可能有些困难,毕竟涉及函数相乘的积分或求和,因此我们尽量从其应用场景来理解卷积的含义。卷积运算在信号处理中有广泛的应用,常常用于计算输入信号经过某个系统处理后得到的输出信号。假设输入信号是
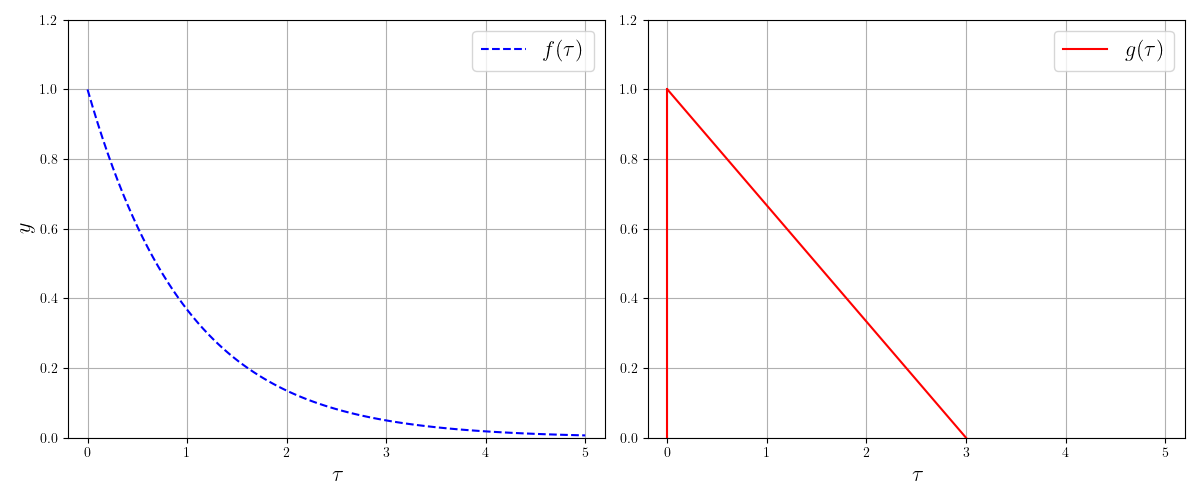
如果将

接下来,随着

我们知道,函数曲线下方的面积可以用积分来计算,该面积为:
上式即为卷积的定义式。如果信号是离散的点,只需要将积分改为求和即可。从这个过程中我们可以看出,卷积的含义是系统
9.2 神经网络中的卷积
在前面的章节中,我们面对图像输入的任务时,常常会想到从图像中提取对任务有帮助的特征,例如图像中不同物体的边界、物体间的相对位置等。如果将图像看作由像素点组成的二维离散信号的话,自然可以借用信号处理中卷积的滤波特性,对图像也做卷积,从而把其中我们想要的特征过滤出来。事实上,用卷积进行图像处理的技术在神经网络之前就已经出现了,而神经网络将其威力进一步增强。
为了在图像上应用卷积,我们先把一维的卷积扩展到二维。由于图像都是离散的,每一个像素有具体的索引,这里我们只给出二维离散卷积的公式:
仔细观察可以发现,该公式还是在计算由
CNN中进行的卷积与实际的卷积有些差异。注意到卷积运算关于
对于神经网络来说,卷积核
该运算称为互相关(cross-correlation),但是在机器学习中,习惯上我们依然称其为卷积。对于图像这样的空间信号来说,我们并不需要像时间信号那样,只有到了特定的时刻才能知道输入信号值。相反,我们可以从图像的任意位置开始处理图像。因此,上式中将求和的下标分别向后推移
至此,我们把卷积的公式做了一些不影响实际结果的变形。可以看出,现在在计算
图9-4给出了一个
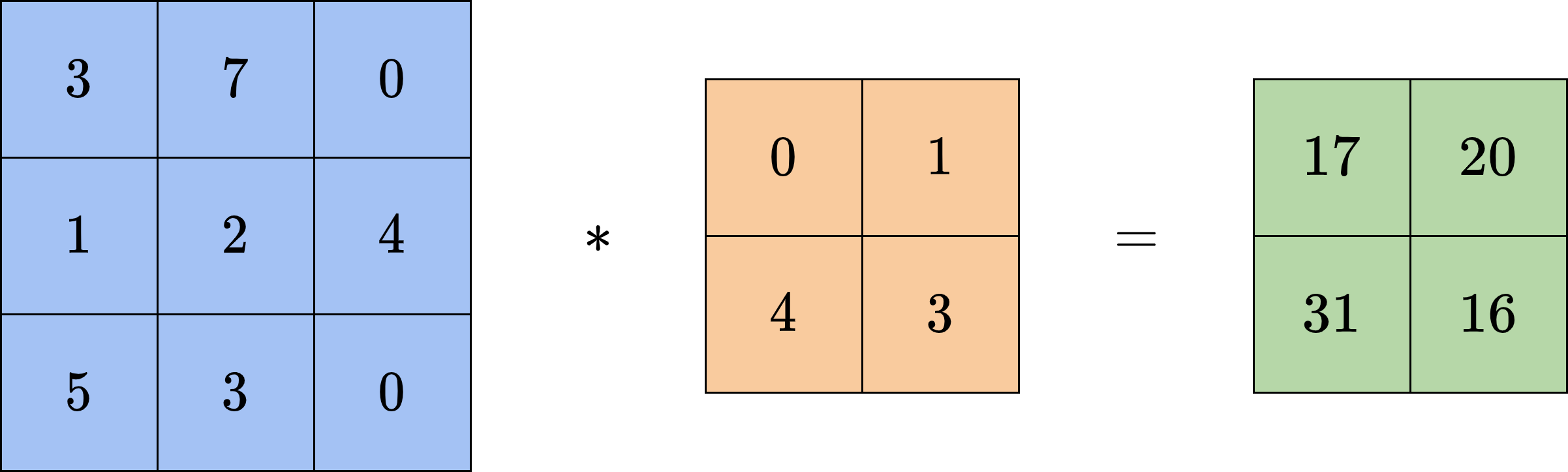
在上面的计算过程中,由于图像边界的存在,卷积得到的结果会比原来的图像更小。设原图宽为
有时候,我们希望输出图像能保持和输入图像同样的大小,因此会对输入图像的周围进行填充(padding),以此抵消卷积对图像尺寸的影响。填充操作会在输入图像四周补上数层额外的像素,假设为了保持图像尺寸不变,需要填充的总层数为:
填充常用的方式有全零填充、常数填充、边界扩展填充等等。其中,全零填充和常数填充即用0或某指定的常数进行填充,边界扩展填充则是将边界处的值向外复制。通常来说,如果
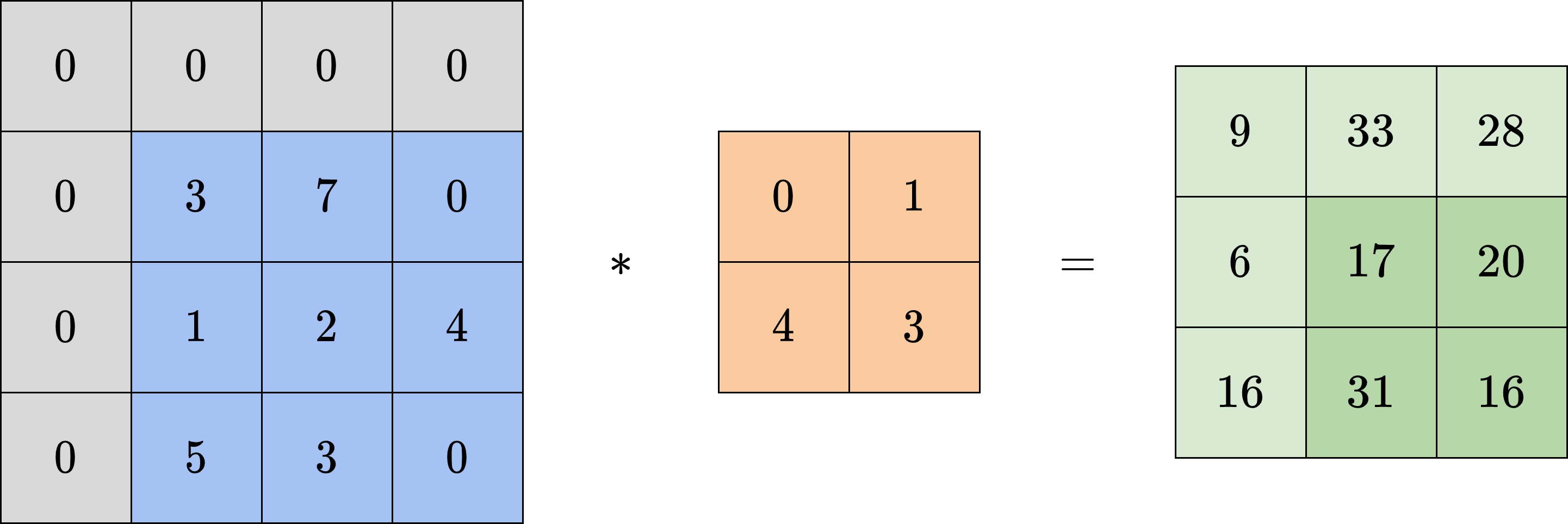
卷积运算可以对一定范围内的图像进行特征提取,其提取范围就是卷积核的大小
除此之外,考虑到图像中通常会有大量相邻的相似像素,在这些区域上进行卷积得到的结果基本是相近的,从而包含大量冗余信息;另一方面,小卷积核对局部的信息可能过于敏感。因此,在卷积之外,我们通常还会对图像进行池化(pooling)操作。池化是一种降采样(downsampling)操作,即用一个代表像素来替代一片区域内的所有像素,从而降低整体的复杂度。常用的池化有平均池化和最大池化两种。顾名思义,平均池化(average pooling)是用区域内所有像素的平均值来代表区域,最大池化(max pooling)是用所有像素的最大值来代表区域。图9-6展示了对4
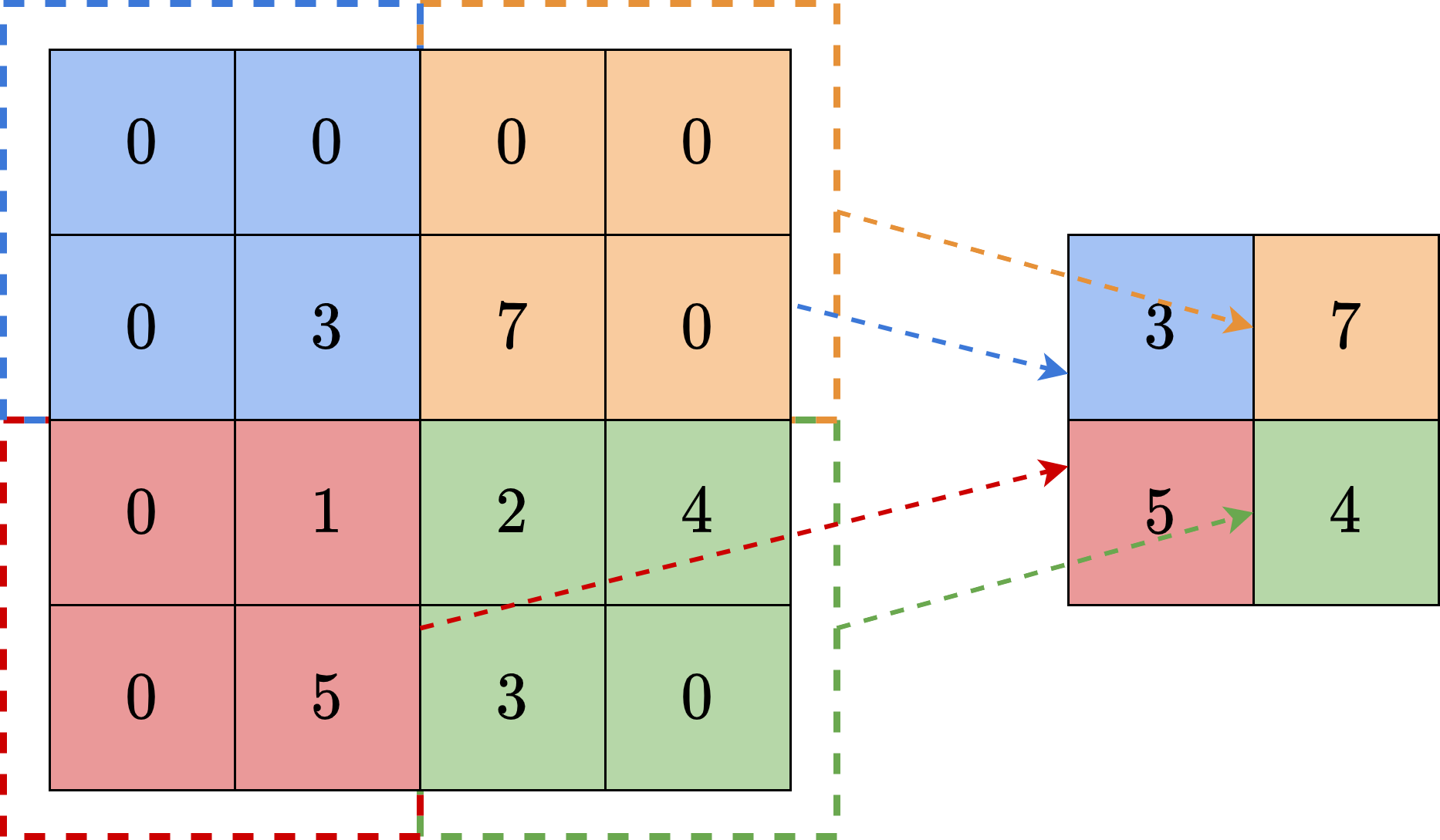
9.3 用卷积神经网络完成图像分类任务
下面,我们讲解如何用PyTorch实现一个卷积神经网络,并用它完成图像分类任务。该任务要求模型能识别输入图像中的主要物体的类别。本次我们采用的 CIFAR-10数据集
表 9-1 CIFAR-10数据集中的图像类别
| 图像标签 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 图像内容 | 飞机 | 汽车 | 鸟 | 猫 | 鹿 | 狗 | 青蛙 | 马 | 船 | 卡车 |
数据集中所有图像大小均为32
import osimport numpy as npimport matplotlib.pyplot as pltfrom tqdm import tqdm # 进度条工具import torchimport torch.nn as nnimport torch.nn.functional as F# transforms提供了数据处理工具import torchvision.transforms as transforms# 由于数据集较大,我们通过工具在线下载数据集from torchvision.datasets import CIFAR10from torch.utils.data import DataLoader
# 下载训练集和测试集data_path = './cifar10'trainset = CIFAR10(root=data_path, train=True,download=True, transform=transforms.ToTensor())testset = CIFAR10(root=data_path, train=False,download=True, transform=transforms.ToTensor())print('训练集大小:', len(trainset))print('测试集大小:', len(testset))# trainset和testset可以直接用下标访问# 每个样本为一个元组 (data, label)# data是3*32*32的Tensor,表示图像# label是0-9之间的整数,代表图像的类别# 可视化数据集num_classes = 10fig, axes = plt.subplots(num_classes, 10, figsize=(15, 15))labels = np.array([t[1] for t in trainset]) # 取出所有样本的标签for i in range(num_classes):indice = np.where(labels == i)[0] # 类别为i的图像的下标for j in range(10): # 展示前10张图像# matplotlib绘制RGB图像时# 图像矩阵依次是宽、高、颜色,与数据集中有差别# 因此需要用permute重排数据的坐标轴axes[i][j].imshow(trainset[indice[j]][0].permute(1, 2, 0).numpy())# 去除坐标刻度axes[i][j].set_xticks([])axes[i][j].set_yticks([])plt.show()
Files already downloaded and verifiedFiles already downloaded and verified训练集大小: 50000测试集大小: 10000

根据上面的讲解,一个基础的CNN主要由卷积核池化两部分构成,如图9-7所示。我们依次用卷积核池化提取图像中不同尺度的特征,最终将最后的类别特征经过全连接层,输出一个10维向量,其每一维分别代表图像属于对应类别的概率。其中,全连接层与我们在MLP中讲过的相同,是前后两层神经元全部互相连接的层,相当于线性变换

在多分类任务中,为了使输出的所有分类概率总和为1,我们常常在输出层使用softmax激活函数。通过softmax得到每一类的概率后,我们再应用最大似然估计的思想。将MLE与softmax结合,得到多分类的交叉熵损失:
其中,
在CNN的发展历程中诞生了许多非常有效的网络结构。其中,2012年由亚历克斯·克里泽夫斯基(Alex Krizhevsky)提出的AlexNet

可以看出,初始时图像有RGB共3种色彩,其通道为3。接下来在卷积和池化的过程中,每次我们都用逐渐变小的卷积核提取图像不同尺度的特征,这也是AlexNet的重要特点之一。同时,图像的大小逐渐变小,但通道逐渐变多,每一个通道都代表一个不同的特征。到全连接层之前,我们已经提取出了64种特征,最后再由全连接层对特征进行分类。与MLP类似,在适当的位置我们会插入非线性激活函数。在第8章我们已经讲过,非线性变换可以增加数据维度,提升模型的表达能力。
除此之外,我们还需要加入丢弃层(dropout)。如图9-9所示,丢弃层会在每次前向传播时,随机把输入中一定比例的神经元遮盖住,使它们对后面的输出不再产生影响,也就不产生梯度回传。对于模型来说,相当于这些神经元暂时“不存在”,从而降低了模型的复杂度,可以缓解模型的过拟合问题。临时遮盖的思想在CNN这样由多层网络组成的复杂模型中尤为重要。
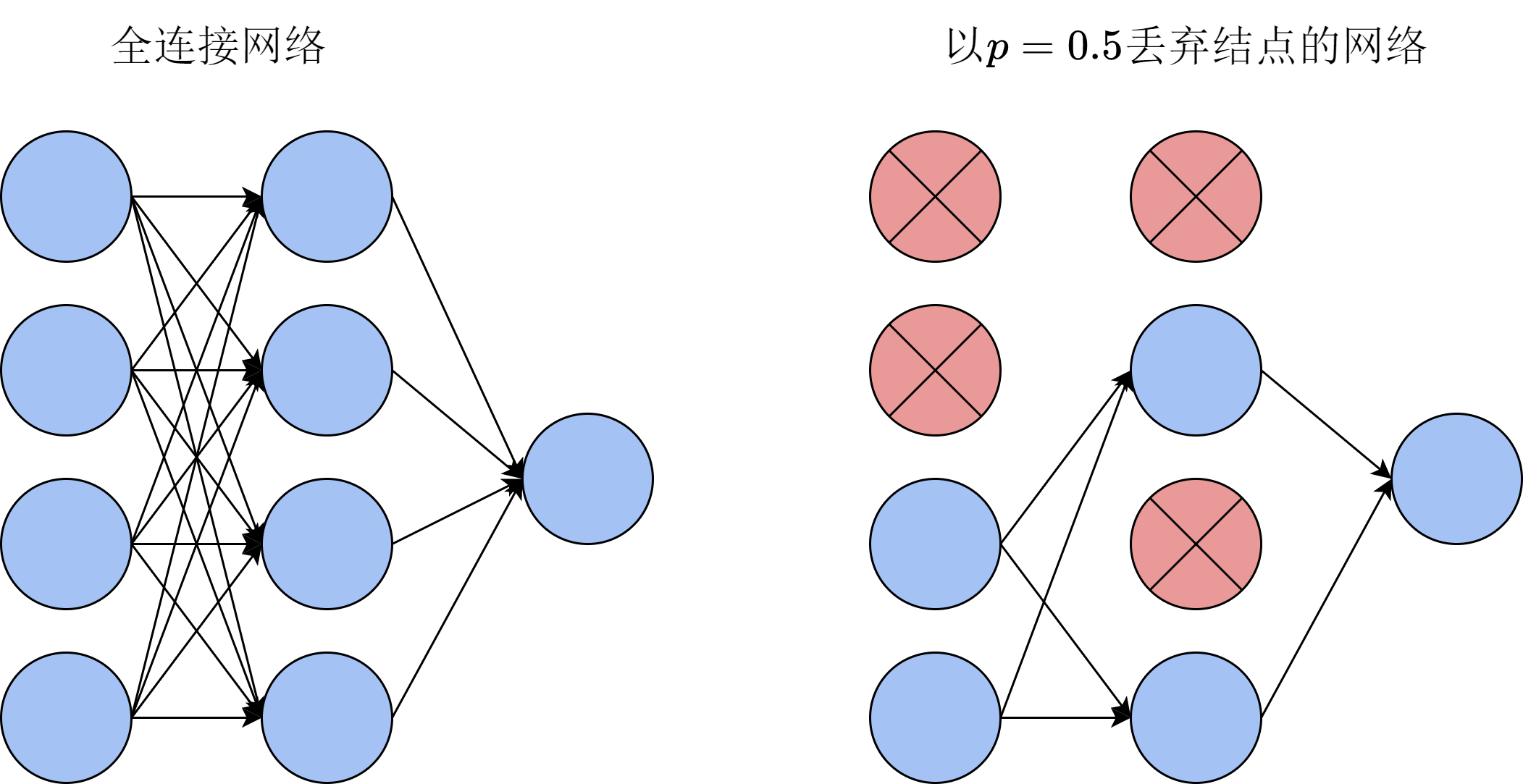
接下来,我们利用PyTorch中的工具,来具体实现图9-8中展示的网络结构。
class CNN(nn.Module):def __init__(self, num_classes=10):super().__init__()# 类别数目self.num_classes = num_classes# Conv2D为二维卷积层,参数依次为# in_channels:输入通道# out_channels:输出通道,即卷积核个数# kernel_size:卷积核大小,默认为正方形# padding:填充层数,padding=1表示对输入四周各填充一层,默认填充0self.conv1 = nn.Conv2d(in_channels=3, out_channels=32,kernel_size=3, padding=1)# 第二层卷积,输入通道与上一层的输出通道保持一致self.conv2 = nn.Conv2d(32, 32, 3, padding=1)# 最大池化,kernel_size表示窗口大小,默认为正方形self.pooling1 = nn.MaxPool2d(kernel_size=2)# 丢弃层,p表示每个位置被置为0的概率# 随机丢弃只在训练时开启,在测试时应当关闭self.dropout1 = nn.Dropout(p=0.25)self.conv3 = nn.Conv2d(32, 64, 3, padding=1)self.conv4 = nn.Conv2d(64, 64, 3, padding=1)self.pooling2 = nn.MaxPool2d(2)self.dropout2 = nn.Dropout(0.25)# 全连接层,输入维度4096=64*8*8,与上一层的输出一致self.fc1 = nn.Linear(4096, 512)self.dropout3 = nn.Dropout(0.5)self.fc2 = nn.Linear(512, num_classes)# 前向传播,将输入按顺序依次通过设置好的层def forward(self, x):x = F.relu(self.conv1(x))x = F.relu(self.conv2(x))x = self.pooling1(x)x = self.dropout1(x)x = F.relu(self.conv3(x))x = F.relu(self.conv4(x))x = self.pooling2(x)x = self.dropout2(x)# 全连接层之前,将x的形状转为 (batch_size, n)x = x.view(len(x), -1)x = F.relu(self.fc1(x))x = self.dropout3(x)x = self.fc2(x)return x
最后,我们设置超参数,利用梯度下降法进行训练。小批量的生成直接使用PyTorch中的DataLoader工具实现。另外,由于本次网络结构比较复杂,较难优化,我们使用SGD优化器的一个改进版本Adam优化器
batch_size = 64 # 批量大小learning_rate = 1e-3 # 学习率epochs = 5 # 训练轮数np.random.seed(0)torch.manual_seed(0)# 批量生成器trainloader = DataLoader(trainset, batch_size=batch_size, shuffle=True)testloader = DataLoader(testset, batch_size=batch_size, shuffle=False)model = CNN()# 使用Adam优化器optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)# 使用交叉熵损失criterion = F.cross_entropy# 开始训练for epoch in range(epochs):losses = 0accs = 0num = 0model.train() # 将模型设置为训练模式,开启dropoutwith tqdm(trainloader) as pbar:for data in pbar:images, labels = dataoutputs = model(images) # 获取输出loss = criterion(outputs, labels) # 计算损失# 优化optimizer.zero_grad()loss.backward()optimizer.step()# 累积损失num += len(labels)losses += loss.detach().numpy() * len(labels)# 精确度accs += (torch.argmax(outputs, dim=-1) \== labels).sum().detach().numpy()pbar.set_postfix({'Epoch': epoch,'Train loss': f'{losses / num:.3f}','Train acc': f'{accs / num:.3f}'})# 计算模型在测试集上的表现losses = 0accs = 0num = 0model.eval() # 将模型设置为评估模式,关闭dropoutwith tqdm(testloader) as pbar:for data in pbar:images, labels = dataoutputs = model(images)loss = criterion(outputs, labels)num += len(labels)losses += loss.detach().numpy() * len(labels)accs += (torch.argmax(outputs, dim=-1) \== labels).sum().detach().numpy()pbar.set_postfix({'Epoch': epoch,'Test loss': f'{losses / num:.3f}','Test acc': f'{accs / num:.3f}'})
100%|████████████████████████████████████| 782/782 [02:21<00:00, 5.53it/s, Epoch=0, Train loss=1.596, Train acc=0.414]100%|██████████████████████████████████████| 157/157 [00:09<00:00, 15.85it/s, Epoch=0, Test loss=1.247, Test acc=0.546]100%|████████████████████████████████████| 782/782 [02:31<00:00, 5.17it/s, Epoch=1, Train loss=1.244, Train acc=0.554]100%|██████████████████████████████████████| 157/157 [00:09<00:00, 16.03it/s, Epoch=1, Test loss=1.061, Test acc=0.631]100%|████████████████████████████████████| 782/782 [02:35<00:00, 5.04it/s, Epoch=2, Train loss=1.086, Train acc=0.613]100%|██████████████████████████████████████| 157/157 [00:10<00:00, 14.68it/s, Epoch=2, Test loss=1.011, Test acc=0.640]100%|████████████████████████████████████| 782/782 [02:28<00:00, 5.28it/s, Epoch=3, Train loss=0.987, Train acc=0.652]100%|██████████████████████████████████████| 157/157 [00:09<00:00, 16.15it/s, Epoch=3, Test loss=0.882, Test acc=0.696]100%|████████████████████████████████████| 782/782 [02:32<00:00, 5.14it/s, Epoch=4, Train loss=0.910, Train acc=0.678]100%|██████████████████████████████████████| 157/157 [00:09<00:00, 15.92it/s, Epoch=4, Test loss=0.842, Test acc=0.708]
小故事: 卷积神经网络来源于神经科学中对生物的视觉系统的研究。1959年,神经科学家大卫·休伯尔(David Hubel)和托斯坦·威泽尔(Torsten Wisesel)提出了感受野的概念,并在1962年通过猫身上的实验确定了感受野等功能的存在。1979年,福岛邦彦(Kunihiko Fukushima)受到其工作的启发,通过神经网络模拟了生物视觉中的感受野,并用不同的层分别提取特征和进行抽象,这就是如今的CNN的雏形。CNN第一次大规模应用是在1998年,杨立昆和本吉奥等人设计的LeNet-5在识别手写数字上取得了巨大成功,并被广泛应用于美国的邮政系统和银行,用来自动识别邮件和支票上的数字。但是,受到当时的硬件条件和技术手段制约,深度神经网络整体在解决复杂问题上遇到困难,CNN研究也沉寂许久。2012年,克里泽夫斯基设计的AlexNet在ImageNet图像分类比赛中以大幅度优势获得第一,确立了CNN在计算机视觉领域的统治地位。2015年,CNN在该比赛中的错误率已经低于了人类水平。
CNN并非只能应用在图像任务上,只要是具有空间关联的输入,都可以通过CNN来提取特征。2016年,由DeepMind公司研制的AlphaGo击败了人类围棋世界冠军李世石九段,让人工智能彻底出圈,成为了家喻户晓的名词。AlphaGo及其后来的改进版本AlphaGo Zero、AlphaZero等模型,都是以CNN为基础进行棋盘特征提取的。此外,CNN还在语音、文本、时间序列等具有一维空间关联的任务上有出色表现。
9.4 用预训练的卷积神经网络完成色彩风格迁移
从CNN的原理上来说,当我们训练完成一个CNN后,其中间的卷积层可以提取出图像中不同类型的特征。进一步分析CNN的结构可以发现,网络前几层的大量卷积和池化层负责将图像特征提取出来,而最后的全连接层和MLP一样,接受提取的特征作为输入,再根据具体的任务目标给出相应的输出。这一发现提醒我们,CNN中的特征提取结构的参数很可能并不依赖于具体任务。在一个任务上训练完成的卷积核,完全可以直接迁移到新的任务上去。在本节中我们就按照这一思路,从预训练好的网络出发,通过微调完成图像的色彩风格迁移任务。值得注意的是,与传统的“对参数求导”的方式不同,本节涉及“对数据求导”的方式来完成图像色彩风格的迁移,这是机器学习中一个重要的思维方式。
9.4.1 VGG 网络
本节采用的预训练网络是另一个广泛应用的CNN结构:VGG网络

9.4.2 内容与风格表示
与KNN一章中自行提取特征的方法不同,现在我们已经可以直接利用训练好的VGG网络提取图像在不同尺度下的各个特征。因此,我们应当考虑的是如何利用这些特征提取结构来完成风格迁移。利用梯度下降的思想,我们可以从一张空白图像或者随机图像出发,通过VGG网络提取其内容和风格特征,与目标的内容图像或者风格图像的相应特征进行比较来计算损失,再通过梯度的反向传播更新输入图像的内容。这样,我们就可以得到内容与内容图像相近、且风格与风格图像相近的结果。
那么,我们该如何使用训练好的VGG网络来提取特征呢?对于CNN来说,从最初的卷积层开始,随着层数加深,网络提取出的特征会越来越侧重于图像整体的风格,以及有关图像中物体相对位置的信息。这是因为图像经过了池化,不同位置的像素被合并在了一起,其精细的信息已经损失了,留下的大多是整体性的信息。图9-11中的内容表示部分是利用VGG16中的5个不同的VGG块对内容图像的一个局部进行处理的结果。可以看出,浅层的卷积核基本只输出原图的像素信息,而深层的卷积核可以输出图像整体的一些抽象结构特征。因此,我们使用VGG16中第5个VGG块的第3个卷积层提取图像的内容。

设提取内容的模型为
相比于内容,图像的风格更难描述,也更不容易直接得到。直观上来说,一张图像的风格指的是图像的色彩、纹理等要素,这些要素在每个尺度上都有体现。因此,我们考虑同一个卷积层中由不同的卷积核提取出的特征。由于这些特征属于同一层,因此基本属于原图中的相同尺度。那么,它们之间的相关性可以一定程度上反映图像在该尺度上的风格特点。设某一层中卷积核的数量为
该矩阵称为格拉姆(Gram)矩阵。矩阵
这里,由于不同卷积层的参数量可能不同,我们额外除以
简单起见,后面我们直接令每一层的权重相等。具体到VGG16中,图9-11的风格表示部分从左至右分别是通过前1至前5个VGG块的第一个卷积层提取的风格信息重建出的图像。可以看出,使用了最多层重建的图像对图像的风格还原度最高,其原因与内容重建中所介绍的类似,不同深度的卷积层提取出的是不同尺度下的特征。小尺度上更偏向纹理,大尺度上更偏向色彩。只有将这些特征全部组合起来,才能得到更完整的图像风格。因此,我们采用全部5个VGG块的第一个卷积层作为风格提取模块。
最终,总的损失函数为:
其中
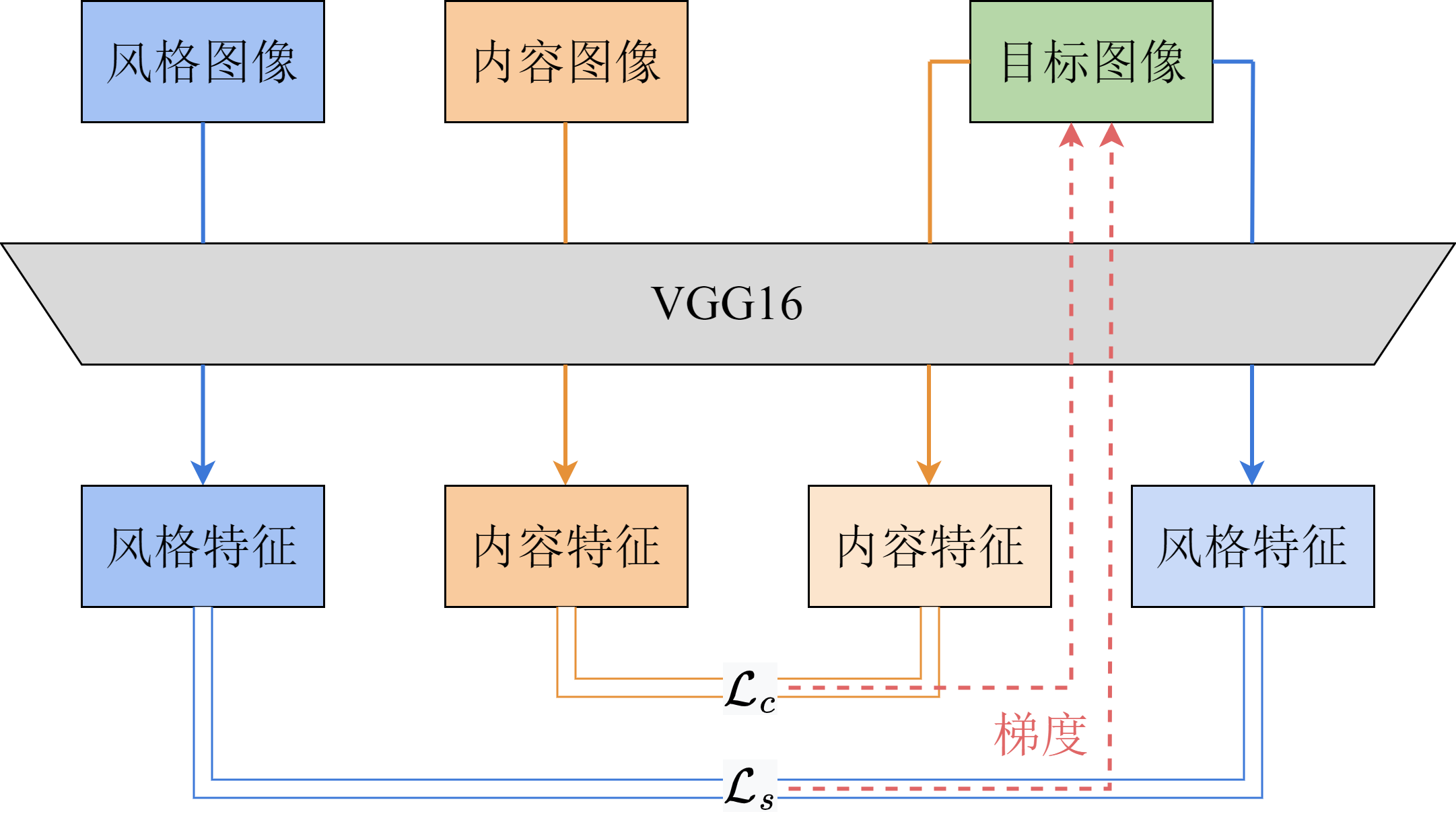
下面,我们来用PyTorch动手完成风格迁移任务。首先导入必要的库,并读取数据集。
# 该工具包中有AlexNet、VGG等多种训练好的CNN网络from torchvision import modelsimport copy# 定义图像处理方法transform = transforms.Resize([512, 512]) # 规整图像形状def loadimg(path):# 加载路径为path的图像,形状为H*W*Cimg = plt.imread(path)# 处理图像,注意重排维度使通道维在最前img = transform(torch.tensor(img).permute(2, 0, 1))# 展示图像plt.imshow(img.permute(1, 2, 0).numpy())plt.show()# 添加batch size维度img = img.unsqueeze(0).to(dtype=torch.float32)img /= 255 # 将其值从0-255的整数转换为0-1的浮点数return imgcontent_image_path = os.path.join('style_transfer', 'content', '04.jpg')style_image_path = os.path.join('style_transfer', 'style.jpg')# 加载内容图像print('内容图像')content_img = loadimg(content_image_path)# 加载风格图像print('风格图像')style_img = loadimg(style_image_path)
内容图像
风格图像
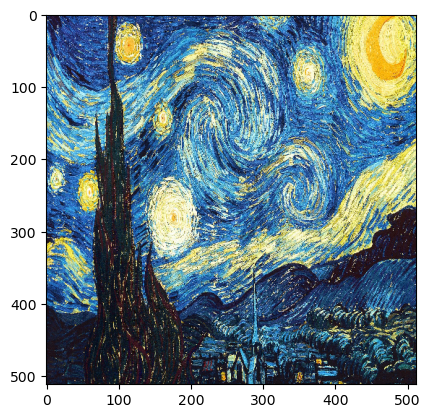
接下来,我们按照上面讲解的方式,定义内容损失和风格损失模块。由于我们后续要在VGG网络上做改动,这里把两种损失都按nn.Module的方式定义。
# 内容损失class ContentLoss(nn.Module):def __init__(self, target):# target为从目标图像中提取的内容特征super().__init__()# 我们不对target求梯度,因此将target从梯度的计算图中分离出来self.target = target.detach()self.criterion = nn.MSELoss()def forward(self, x):# 利用MSE计算输入图像与目标内容图像之间的损失self.loss = self.criterion(x.clone(), self.target)return x # 只计算损失,不改变输入def backward(self):# 由于本模块只包含损失计算,不改变输入,因此要单独定义反向传播self.loss.backward(retain_graph=True)return self.lossdef gram(x):# 计算G矩阵batch_size, n, w, h = x.shape # n为卷积核数目,w和h为输出的宽和高f = x.view(batch_size * n, w * h) # 变换为二维g = f @ f.T / (batch_size * n * w * h) # 除以参数数目,进行归一化return g# 风格损失class StyleLoss(nn.Module):def __init__(self, target):# target为从目标图像中提取的风格特征# weight为设置的强度系数lambdasuper().__init__()self.target_gram = gram(target.detach()) # 目标的Gram矩阵self.criterion = nn.MSELoss()def forward(self, x):input_gram = gram(x.clone()) # 输入的Gram矩阵self.loss = self.criterion(input_gram, self.target_gram)return xdef backward(self):self.loss.backward(retain_graph=True)return self.loss
然后,我们下载已经训练好的VGG16网络,并按照其结构抽取我们需要的卷积层,舍弃最后与原始任务高度相关的全连接层,但将激活函数和池化层保持原样。我们将抽出的层依次加入到一个新创建的模型中,供后续提取特征使用。
vgg16 = models.vgg16(weights=True).features # 导入预训练的VGG16网络# 选定用于提取特征的卷积层,Conv_13对应着第5块的第3卷积层content_layer = ['Conv_13']# 下面这些层分别对应第1至5块的第1卷积层style_layer = ['Conv_1', 'Conv_3', 'Conv_5', 'Conv_8', 'Conv_11']content_losses = [] # 内容损失style_losses = [] # 风格损失model = nn.Sequential() # 储存新模型的层vgg16 = copy.deepcopy(vgg16)index = 1 # 计数卷积层# 遍历 VGG16 的网络结构,选取需要的层for layer in list(vgg16):if isinstance(layer, nn.Conv2d): # 如果是卷积层name = "Conv_" + str(index)model.append(layer)if name in content_layer:# 如果当前层用于抽取内容特征,则添加内容损失target = model(content_img).clone() # 计算内容图像的特征content_loss = ContentLoss(target) # 内容损失模块model.append(content_loss)content_losses.append(content_loss)if name in style_layer:# 如果当前层用于抽取风格特征,则添加风格损失target = model(style_img).clone()style_loss = StyleLoss(target) # 风格损失模块model.append(style_loss)style_losses.append(style_loss)if isinstance(layer, nn.ReLU): # 如果激活函数层model.append(layer)index += 1if isinstance(layer, nn.MaxPool2d): # 如果是池化层model.append(layer)# 输出模型结构print(model)
Sequential((0): Conv2d(3, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))(1): StyleLoss((criterion): MSELoss())(2): ReLU(inplace=True)(3): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))(4): ReLU(inplace=True)(5): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)(6): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))(7): StyleLoss((criterion): MSELoss())(8): ReLU(inplace=True)(9): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))(10): ReLU(inplace=True)(11): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)(12): Conv2d(128, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))(13): StyleLoss((criterion): MSELoss())(14): ReLU(inplace=True)(15): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))(16): ReLU(inplace=True)(17): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))(18): ReLU(inplace=True)(19): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)(20): Conv2d(256, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))(21): StyleLoss((criterion): MSELoss())(22): ReLU(inplace=True)(23): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))(24): ReLU(inplace=True)(25): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))(26): ReLU(inplace=True)(27): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)(28): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))(29): StyleLoss((criterion): MSELoss())(30): ReLU(inplace=True)(31): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))(32): ReLU(inplace=True)(33): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))(34): ContentLoss((criterion): MSELoss())(35): ReLU(inplace=True)(36): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False))
现在我们已经以VGG16为基础定义了自己的新模型。应当始终注意,我们并不关心模型的输出,也不会对输出计算任何损失函数。我们所关心的部分只有模型中计算内容损失和风格损失的模块,所有的梯度也是从这些层中产生的。最后,我们设置超参数,并训练模型,查看生成图像的效果。
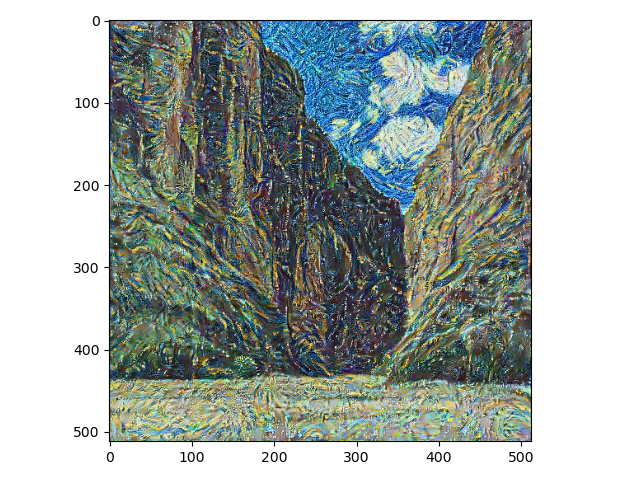
epochs = 200learning_rate = 0.1lbd = 1e6 # 强度系数input_img = content_img.clone() # 从内容图像开始迁移param = nn.Parameter(input_img.data) # 将图像内容设置为可训练的参数optimizer = torch.optim.Adam([param], lr=learning_rate) # 使用Adam优化器for i in range(epochs):style_score = 0 # 本轮的风格损失content_score = 0 # 本轮的内容损失model(param) # 将输入通过模型,得到损失for cl in content_losses:content_score += cl.backward()for sl in style_losses:style_score += sl.backward()style_score *= lbdloss = content_score + style_score# 更新输入图像optimizer.zero_grad()loss.backward()optimizer.step()# 每次对输入图像进行更新后# 图像中部分像素点会超出0-1的范围# 因此要对其进行剪切param.data.clamp_(0, 1)if i % 10 == 0 or i == epochs - 1:print(f'训练轮数:{i},\t风格损失:{style_score.item():.4f},\t' \f'内容损失:{content_score.item():.4f}')plt.imshow(input_img[0].permute(1, 2, 0).numpy())plt.show()
训练轮数:0, 风格损失:11691.9434, 内容损失:0.0000
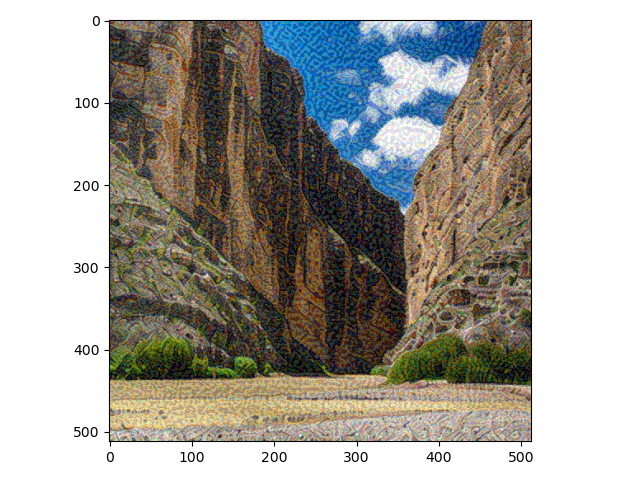
训练轮数:50, 风格损失:88.6561, 内容损失:3.3538
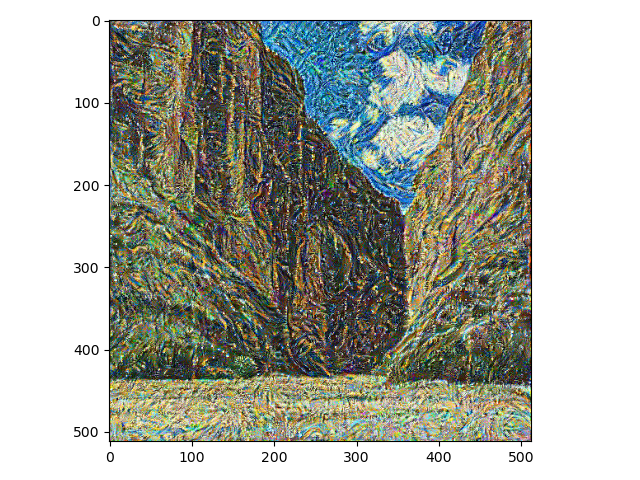
训练轮数:100, 风格损失:21.4739, 内容损失:2.5380
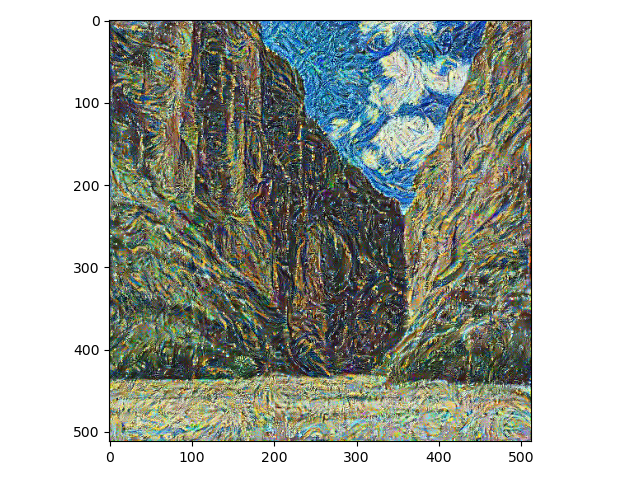
训练轮数:150, 风格损失:12.5777, 内容损失:2.2838
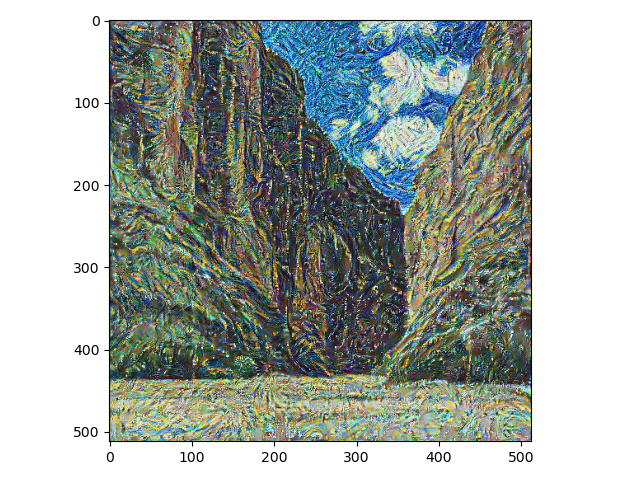
训练轮数:199, 风格损失:24.1864, 内容损失:1.9889
9.5 本章小结
本章介绍了卷积神经网络和其在图像处理任务中的应用。作为人工智能划时代的一页,能够有效应用的CNN在图像任务上的出色表现逐渐让人工智能走进了大众视野。除了图像之外,CNN捕捉不同尺度特征的能力在自然语言处理中也有广泛应用,我们可以用它来提取文本中上下文的背景内容,从而让模型对文本有更准确的理解。在本章的第二个任务中,我们展示了CNN中各层网络的作用,不同深度的卷积层可以提取不同尺度和类型的图像特征。这也启发我们,神经网络训练中得到的网络参数并非一些杂乱无章的数字,而有其具体含义。因此,对于更加复杂的网络来说,其可解释性仍然是研究的重要一环。另外,将训练好的CNN中我们需要的层提取出来用于新任务的做法,可以避免从零训练网络产生的大量时间和资源开销。在深度学习时代,随着模型复杂度不断增大,像这样应用预训练模型(pre-trained model)的做法越来越广泛。而如何更好地利用预训练模型完成特定任务,已经成为深度学习领域重要的研究课题之一。
习题
以下关于CNN的说法正确的是: A. 卷积运算考虑了二维的空间信息,所以CNN只能用来完成图像相关的任务。 B. 池化操作进行了降采样,将会丢弃部分信息,影响模型效果。 C. 由卷积层得到的特征也需要经过非线性激活函数,来提升模型的表达能力。 D. 填充操作虽然保持了输出的尺寸,但是引入了与输入无关的信息,干扰特征提取。
以下关于CNN中卷积层和池化层的描述正确的是: A. 卷积层和池化层必须交替出现。 B. 池化层只有最大池化和平均池化两种。 C. 池化层的主要目的之一是为了减少计算复杂度。 D. 卷积层中有许多不同的卷积核,每个卷积核在输入的一部分区域上做运算,合起来覆盖完整的输入。
CNN的卷积层中还有一个常用参数是步长(stride),表示计算卷积时,卷积核每次移动的距离。在图9-5的示例中,卷积核每次移动一格,步长为1,它的左上角经过
至 共9个点。如果将步长改为2,卷积核每次移动两格,左上角只经过 共4个点,以此类推。假设输入宽为 ,在宽度方向填充长度 。卷积核宽为 ,在宽度方向的步长为 。假设所有除法都可以整除,推导卷积后输出矩阵的宽度 。 试调整上述AlexNet网络的层数、卷积核的大小和数量、丢弃率等设置,观察其训练性能的改变。
试调整图像色彩风格迁移中的
权重,也即修改代码中 lbd的取值,观察输出图像的变化。针对图像色彩风格迁移任务,思考除了上述
的方式来刻画图像色彩风格,是否还有其他刻画方式?试实现一种新的图像风格损失函数,并观察其效果。
参考文献
[1] CIFAR-10数据集:Krizhevsky A, Hinton G. Learning multiple layers of features from tiny images[J]. 2009.
[2] LeNet-5论文:LeCun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324.
[3] AlexNet论文:Krizhevsky A, Sutskever I, Hinton G E. Imagenet classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 60(6): 84-90.
[4] Adam论文:Kingma D P, Ba J. Adam: A method for stochastic optimization[J]. arXiv preprint arXiv:1412.6980, 2014.
[5] VGG论文:Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition[J]. arXiv preprint arXiv:1409.1556, 2014.
[6] 图片来自论文:Gatys L A, Ecker A S, Bethge M. Image style transfer using convolutional neural networks[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 2414-2423.
[7] CNN对纹理和轮廓的偏好:Geirhos R, Rubisch P, Michaelis C, et al. ImageNet-trained CNNs are biased towards texture; increasing shape bias improves accuracy and robustness[C]//International Conference on Learning Representations. 2019.
拓展阅读:数据增强
在第5章中我们讲过,模型的复杂度应当和数据的复杂度相匹配,否则就很容易出现欠拟合或过拟合的情况。对于深度神经网络来说,其参数量非常庞大。然而,高质量的训练样本又非常稀缺,许多时候要依赖人工标注,费时费力,这使得神经网络的复杂度往往会超过数据的复杂度,从而发生过拟合的情况。因此,防止神经网络的过拟合是现代机器学习算法研究中的一个重要课题。我们已经知道,通过引入正则化、丢弃层等方式可以限制模型的复杂度。另一方面,我们也可以从数据的角度出发,通过适当地扩充数据集来增加数据的复杂度:引入许多原本在数据集中不存在、但是又同样合理的数据,提升模型的泛化性能,降低过拟合的程度,这就是数据增强(data augmentation)技术。
我们以图像任务为例进行简单介绍。在第2章里,我们使用KNN完成了手写数字识别任务。当然,CNN可以做得更好。但是假设图像中的背景不再是黑色,而是每种数字都有一个独特的颜色,比如1是蓝色、2是红色、3是绿色等等,再让CNN在这样的数据集上训练,它会学到数据中的什么关联呢?接下来,如果把红色背景的1输入给模型进行测试,模型会把它识别成1还是2呢?实验表明,CNN更多地依赖图像的纹理、颜色来识别图像,而非图像的轮廓
为了解决类似的问题,我们常常会在训练时对图像进行一定的变换,从而生成一系列相似、但又不相同的图像,如图9-13所示:
- 旋转与翻转:把图像旋转一定的角度或进行水平、竖直翻转。
- 随机裁剪:保留图像核心内容的前提下,随机裁掉一定的边缘部分,再放大至原始大小。
- 缩放:将图像放大或缩小。放大后超出原始大小的部分裁减掉,缩小后不足的部分用常数或其他方式填充。
- 改变颜色:通过算法调整图像的色调、亮度、对比度等颜色信息。
- 添加噪声:在图像中随机添加噪点,例如高斯噪声。

需要注意,并非所有的图像数据增强方法都适用于所有任务。例如在本章用到的CIFAR-10数据集中,飞机的图像旋转90°还是飞机,汽车的图像水平翻转后还是汽车;但在MNIST数据集中,数字1旋转90°后就不再是数字1了,数字6旋转180°更是变成了数字9。因此,旋转与翻转方法在后者上就不适用。在实际应用中,我们需要根据任务的具体要求和图像特点,选择合适的数据增强方法。9.3节中,我们用简化的AlexNet在CIFAR-10上达到了70%左右的分类准确率。感兴趣的读者可以尝试用合适的方法进行数据增强,从而大幅提升模型表现,预计在测试集上有75%以上的准确率。
并非只有图像数据可以进行数据增强。在文本任务中,我们可以通过对词语做同义词替换、选择性遮盖句子的部分成分、将句子翻译成其他语言再翻译回来等方式,得到新的训练文本。事实上,数据增强在各种类型的机器学习任务中都有广泛应用,更有许多算法将数据增强的部分与模型合为一体,它已经成为了现代机器学习中提升数据利用率和提升模型泛化性能的关键技术。