第 14 章 k均值聚类

本章开始我们讲解无监督学习算法。在之前的章节中，我们给模型的任务通常是找到样本与标签之间的对应关系。在训练时，模型对样本给出预测，再通过损失函数计算与之间的偏差，从而优化模型。在这一过程中，真实标签保证我们可以根据模型的预测来调整模型，起到了“监督”模型输出的作用。因此，这样的学习过程称为监督学习（supervised learning）。还有一类任务中，我们只有样本，却没有其标签。这类任务也不再是通过去预测，而是通过样本的特征找到样本之间的关联。由于没有标签作为监督信号，这一过程被称为无监督学习（unsupervised learning）。监督学习和无监督学习在某些情况下可以互相转化。例如在卷积神经网络一章中，我们通过训练集中的图像与其类别得到模型，在测试集上完成了图像分类任务，这是有监督学习的过程。我们最后给图像分类的依据是由模型提取出的图像的特征。然而，即使我们一开始就不知道图像的真实类别，也可以通过图像特征之间的相似程度判断出来哪些图像属于同一类。也就是说，我们可以在仅有图像的情况下把猫和狗的图像分为两类，而类别无非是告诉我们这两类分别叫“猫”和“狗”而已。

本章我们将要讲解的k均值（k-means）聚类算法就是一个无监督学习算法。它的目标是将数据集中的样本根据其特征分为几个类，使得每一类内部样本的特征都尽可能相近，这样的任务通常称为聚类任务。作为最简单的聚类算法，k均值算法在现实中有广泛的应用。下面，我们就来详细讲解k均值算法的原理。

14.1 k均值聚类的原理

假设空间中有一些点，聚类问题的目标就是将这些点按距离分成数类。设数据集，其中每个样本的特征维数都是。最终聚簇的个数由我们提前指定。直观上来说，同一类的点之间距离应该比不同类的点之间的距离远。但是，由于我们没有任何点的真实标签，所以也无法在最开始确定每一类的中心（centroid），以其为基准计算距离并分类。针对这一问题，k均值算法提出了一个非常简单的解决方案：在初始时，随机选取数据集中的个点，将作为第类的中心。选取中心后，我们用最简单的方式，把数据集中的点归到最近的中心点所代表的类中。记第类包含样本的集合为，两点之间的距离函数为，那么可以写为：

当然，仅仅随机选取中心点还不够，我们还要继续进行优化，尽可能减小类内的点到中心点距离。将数据集中所有点到其对应中心距离之和作为损失函数，得到：

既然在初始时，各个类的中心点是随机选取的，那么我们应当再选取新的中心点，使得损失函数的值最小。将上式对求偏导，得：

如果我们用欧氏距离的平方作为度量标准，上式可以进一步计算为：

令该偏导数为零，就得到最优的中心点为：

该式表明，最优中心点就是中所有点的重心。但是，当中心点更新后，每个样本距离最近的中心点可能也会发生变化。因此，我们重新计算每个样本点到中心点的距离，对它们重新分类，再计算新的重心。如此反复迭代，直到各个点的分类几乎不再变化或者达到预设的迭代次数位置。需要注意，如果采用其他的距离函数作为度量，那么最优的中心点就不再是集合的重心。

14.2 动手实现k均值算法

下面，我们用一个简单的平面点集kmeans_data.csv来展示k均值聚类算法的效果。首先，我们加载数据集并可视化。数据集中每行包含两个值和，表示平面上坐标为的点。考虑到我们还希望绘制迭代的中间步骤，这里将绘图部分写成一个函数。

import numpy as np
import matplotlib.pyplot as plt

dataset = np.loadtxt('kmeans_data.csv', delimiter=',')
print('数据集大小：', len(dataset))

数据集大小： 80

# 绘图函数
def show_cluster(dataset, cluster, centroids=None):  
    # dataset：数据
    # centroids：聚类中心点的坐标
    # cluster：每个样本所属聚类
    # 不同种类的颜色，用以区分划分的数据的类别
    colors = np.array(['blue', 'red', 'green', 'purple'])
    # 画出所有样例
    plt.scatter(dataset[:, 0], dataset[:, 1], color=colors[cluster])

    # 画出中心点
    if centroids is not None:
        K = len(centroids)
        plt.scatter(centroids[:, 0], centroids[:, 1], 
            color=colors[:K], marker='+', s=150)  

    plt.show()

# 初始时不区分类别
show_cluster(dataset, np.zeros(len(dataset), dtype=int))

​
​

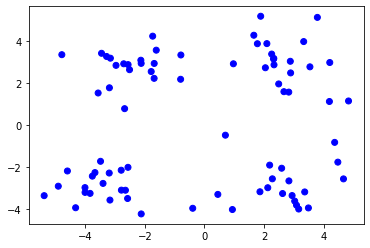
对于简单的k均值算法，初始的中心点是从现有样本中随机选取的，我们将其实现如下。

def random_init(dataset, K):
    # 随机选取是不重复的
    idx = np.random.choice(np.arange(len(dataset)), size=K, replace=False)
    return dataset[idx]

接下来，我们用欧氏距离作为标准，实现上面描述的迭代过程。由于数据集比较简单，我们将迭代的终止条件设置为所有点的分类都不再变化。对于更复杂的数据集，这一条件很可能无法使迭代终止，从而需要我们控制最大迭代次数，或者设置允许类别变动的点的比例等等。

def Kmeans(dataset, K, init_cent):
    # dataset：数据集
    # K：目标聚类数
    # init_cent：初始化中心点的函数
    centroids = init_cent(dataset, K)
    cluster = np.zeros(len(dataset), dtype=int)
    changed = True
    # 开始迭代
    itr = 0
    while changed:
        changed = False
        loss = 0
        for i, data in enumerate(dataset):
            # 寻找最近的中心点
            dis = np.sum((centroids - data) ** 2, axis=-1)
            k = np.argmin(dis)
            # 更新当前样本所属的聚类
            if cluster[i] != k:
                cluster[i] = k
                changed = True
            # 计算损失函数
            loss += np.sum((data - centroids[k]) ** 2)
        # 绘图
        print(f'Iteration {itr}, Loss {loss:.3f}')
        show_cluster(dataset, cluster, centroids)
        # 更新中心点
        for i in range(K):
            centroids[i] = np.mean(dataset[cluster == i], axis=0)
        itr += 1

    return centroids, cluster

最后，我们观察k均值算法在上面的数据集上聚类的过程。根据上面的可视化结果，我们大概可以看出有4个聚类，因此设定。

np.random.seed(0)
cent, cluster = Kmeans(dataset, 4, random_init)

Iteration 0, Loss 711.345

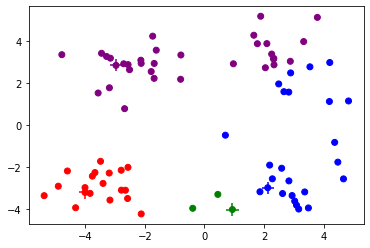
Iteration 1, Loss 409.497

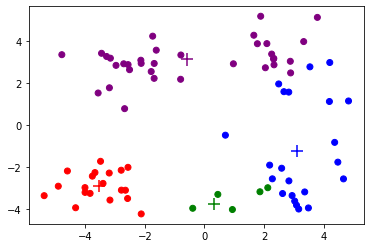
Iteration 2, Loss 395.266

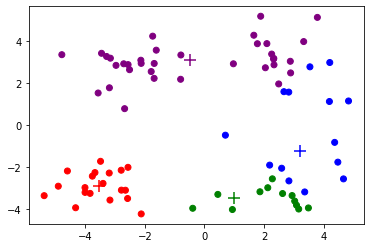
Iteration 3, Loss 346.070

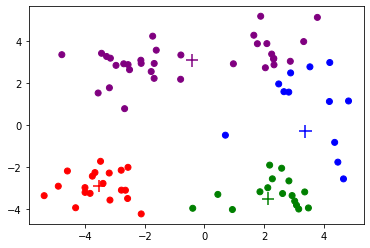
Iteration 4, Loss 294.243

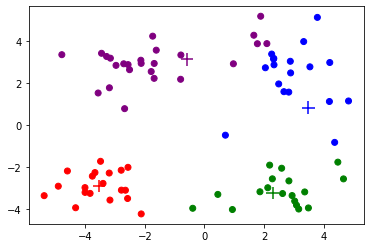
Iteration 5, Loss 178.808

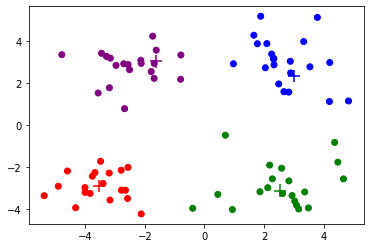
Iteration 6, Loss 151.089

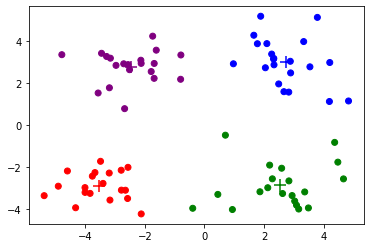
14.3 k-means++

上面的分类结果与我们的主观感受区别不大。但是，k均值算法对初始选择的聚类中心非常敏感，且极易收敛到局部最小值，因此不同的中心选择可能导致完全不同的划分。通常来说，我们可以用不同的随机种子选择多组初值，最终挑出划分最好的那一个。但是，当聚类个数和数据量较大时，k均值算法运行需要的时间很长，反复调整随机种子也很不方便。因此，k-means++算法提出了一种新的初始中心选择方法，使算法整体对随机种子的依赖大大减小。

首先，k-means++算法从所有样本中随机选取一个点当作第一个聚类的中心点。直观上来讲，我们希望初始的中心点尽可能散开。因此在选择接下来的中心点时，该算法会将样本到当前中心点的距离也纳入考量。设目前已有个中心点，分别是，对于样本，其他与最近的中心点的距离为。为了使各个中心点之间的距离尽可能大，令被选为第个中心点的概率为：

上式的分母是在整个数据集上进行的求和，使所有样本被选为中心点的概率值和为。上式的含义是，样本被选为中心点的概率与其到当前中心点距离的平方成正比。我们重复这一过程，直到个聚类中心都被选出为止。

下面，我们来实现k-means++的初始化函数。

def kmeanspp_init(dataset, K):
    # 随机第一个中心点
    idx = np.random.choice(np.arange(len(dataset)))
    centroids = dataset[idx][None]
    for k in range(1, K):
        d = []
        # 计算每个点到当前中心点的距离
        for data in dataset:
            dis = np.sum((centroids - data) ** 2, axis=-1)
            # 取最短距离的平方
            d.append(np.min(dis) ** 2)
        # 归一化
        d = np.array(d)
        d /= np.sum(d)
        # 按概率选取下一个中心点
        cent_id = np.random.choice(np.arange(len(dataset)), p=d)
        cent = dataset[cent_id]
        centroids = np.concatenate([centroids, cent[None]], axis=0)

    return centroids

我们已经预留了初始化函数的接口，只需要将参数从random_init替换为kmeanspp_init就可以测试k-means++算法的表现了。从绘制的迭代中间结果可以明显看出，用k-means++算法选择的初始中心点互相之间的距离非常远，从而收敛速度也要快很多。读者可以修改随机种子，观察随机初始化和k-means++初始化对随机种子的敏感程度。

cent, cluster = Kmeans(dataset, 4, kmeanspp_init)

Iteration 0, Loss 373.941

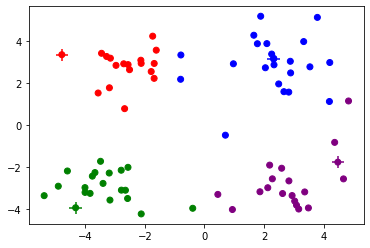
Iteration 1, Loss 158.147

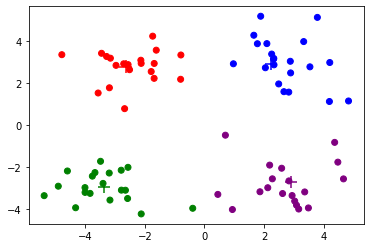
Iteration 2, Loss 151.273

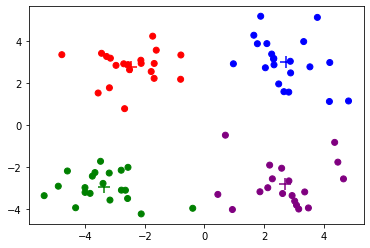
14.4 本章小结

本章主要介绍了k均值聚类算法和其改进版k-means++。k均值算法由于其简单易用，应用非常广泛。然而，它也高度依赖于初始中心和距离函数的选取。上面的k-means++就是在初始中心点选取的方式上做了改进。对于距离函数来说，它起到判断哪些样本之间的距离较近的关键作用，因此也要随数据集的特征而灵活调整。在上面的平面点集任务中，我们选用了最简单的欧氏距离。而当数据的特征维度较高时，简单的欧氏距离会面临维数灾难问题。简单来说，在高维空间中，数据点会变得越来越稀疏，任意两个数据点之间的欧氏距离都差别不大，欧氏距离失去了判断相似度的功能。因此，当数据的特征维度更高、关系更复杂的时候，距离函数需要精心设计，甚至要通过神经网络训练得到。因此，k均值聚类算法通常不会作为复杂聚类任务的第一步，而是在其他算法挑选出数据的关键特征、得到合适的距离函数后，再进行最后的聚类工作。

网站Cartography Playground给出了在平面点集上应用k均值算法的动画演示和结果，感兴趣的读者还可以自行调整数据集，观察迭代过程中中心点和聚类的变化，加深对k均值算法的理解。

习题

1. k均值算法收敛得到的解一定是局部最优吗？一定是全局最优吗？ A. 是 B. 不是

2. 如果设定的值比数据中实际的类别要少，会造成什么情况？是否有办法在不知道数据包含几类的情况下，选出合适的值？

3. k均值算法的结果及其依赖于初始中心的选取，从而对随机种子非常敏感。试构造一个数据集，在的情况下，存在至少两组 K 均值算法可能收敛到的聚类中心，且数据的分类不同。如果换成k-means++算法，在该数据集上收敛的结果是否唯一？

4. 除了k-means++以外，k均值算法还有一种改进，称为二分k均值。该算法首先将所有数据看作一类。接下来每次迭代中，找到类内部所有点距离之和

最大的类，再将该类分成两个使得类内距离之和下降最多的子类。如此循环，直到类的数量达到预先指定的为止。实现该算法，并在14.2节中的数据集上测试。

5. 设计一种新的距离度量函数，实现基于该度量函数的k-means和k-means++，并在14.2节中的数据集上测试。

6. 查阅相关文献，学习并实现DBSCAN聚类算法，并和k-means、k-means++对比。

参考文献

[1] k-means++论文：Arthur D, Vassilvitskii S. k-means++: The advantages of careful seeding[R]. Stanford, 2006.

[2] DBSCAN论文：Ester M, Kriegel H P, Sander J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[C]//kdd. 1996, 96(34): 226-231.