动手学机器学习

第 3 章 k 近邻算法

本章开始，我们先来讲解两个最简单的机器学习算法，从中展开机器学习的一些基本概念和思想。或许有的读者会认为机器学习非常困难，需要庞大的模型、复杂的网络，但事实并非如此。相当多的机器学习算法都非常简单、直观，也不涉及神经网络。本章就将介绍一个最基本的分类和回归算法：k 近邻（k-nearest neighbor, KNN）算法。KNN 是最简单也是最重要的机器学习算法之一，它的思想可以用一句话来概括：“相似的数据往往拥有相同的类别”，这也对应于中国的一句谚语：“物以类聚，人以群分”。具体来说，我们在生活中常常可以观察到，同一种类的数据之间特征更为相似，而不同种类的数据之间特征差别更大。例如，在常见的花中，十字花科的植物大多数有 4 片花瓣，而夹竹桃科的植物花瓣大多数是 5 的倍数。虽然存在例外，但如果我们按花瓣数量对植物做分类，那么花瓣数量相同或成倍数关系的植物，相对更可能属于同一种类。

下面，本章将详细讲解并动手实现 KNN 算法，再将其应用到不同的任务中去。

3.1 KNN 算法的原理

在分类任务中，我们的目标是判断样本的类别。KNN 首先会观察与该样本点距离最近的个样本，统计这些样本所属的类别。然后，将当前样本归到出现次数最多的类中。我们用 KNN 算法的一张经典示意图来更清晰地说明其思想。如图 3-1 所示，假设共有两个类别的数据点：蓝色圆形和橙色正方形，而中心位置的绿色样本当前尚未被分类。根据统计近邻的思路：

  • 当时，绿色样本的个近邻中有两个橙色正方形样本，一个蓝色圆形样本，因此应该将绿色样本点归类为橙色正方形。
  • 当时，绿色样本的个近邻中有两个橙色正方形样本，三个蓝色圆形样本，因此应该将绿色样本点归类为蓝色圆形。
knn
图 3-1 KNN 算法示意图

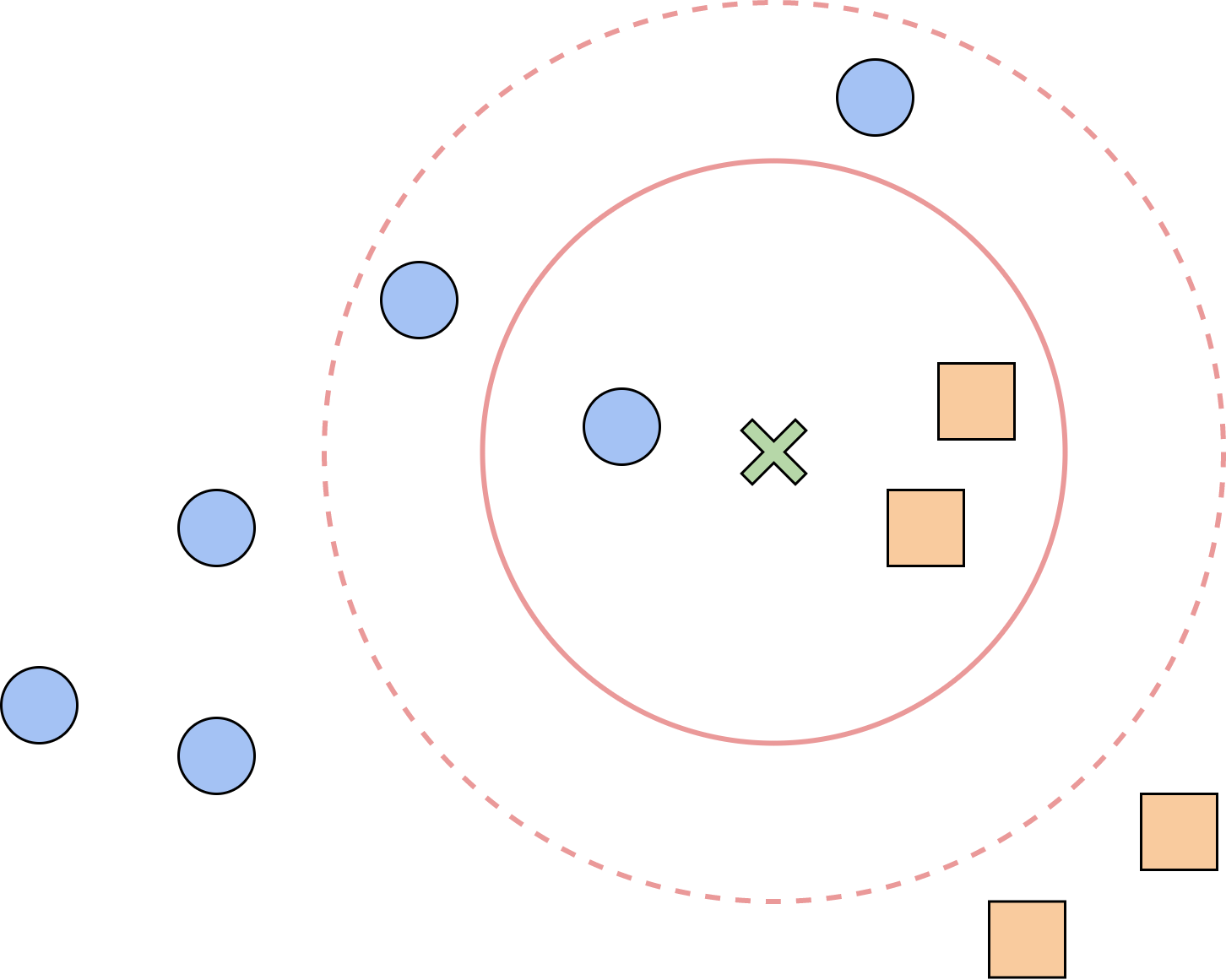
从这个例子中可以看出，KNN 的基本思路是让当前样本的分类服从邻居中的多数分类。但是，当的大小变化时，由于邻居的数量变化，其多数类别也可能会变化，从而改变对当前样本的分类判断。因此，决定的大小是 KNN 中最重要的部分之一。直观上来说，当的取值太小时，分类结果很容易受到待分类样本周围的个别噪声数据影响；当的取值太大时，又可能将远处一些不相关的样本包含进来。因此，我们应该根据数据集动态地调整的大小，以得到最理想的结果。

下面，我们用数学语言来描述 KNN 算法。设已分类样本的集合为。对于一个待分类的样本，定义其邻居为中与距离最近的个样本组成的集合，这些样本对应的类别分别是。我们统计集合中类别为的样本的数量，记为：

其中，是示性函数，其自变量是一个命题。当为真时，反之，当为假时。最后，我们将的类别判断为使最大的类别：

与分类任务类似，我们还可以将 KNN 应用于回归任务。对于样本，我们需要预测其对应的实数值。同样的，KNN 考虑个相邻的样本点，将这些样本点对应的实数值进行加权平均，就得到样本的预测结果。

在这里，权重代表不同邻居对当前样本的重要程度，权重越大，该邻居的值对最后的预测影响也越大。我们既可以预先定义好权重，例如简单地认为所有邻居的重要程度相同，令所有；也可以根据数据集的特性设置权重与距离的关系，例如让权重与距离成反比；还可以将权重作为模型的参数，通过学习得到。

3.2 用 KNN 算法完成分类任务

本节将在 MNIST 数据集上应用 KNN 算法，完成分类任务。MNIST 是手写数字数据集，其中包含了很多手写数字 0~9 的黑白图像，每张图像都由 2828 个像素点组成。读者可以在 MNIST 的官方网站上得到更多数据集的信息。读入后，每个像素点用 1 或 0 表示，1 代表黑色像素，属于图像背景；0 代表白色像素，属于手写数字。我们的任务是用 KNN 对不同的手写数字进行分类。为了更清晰地展示数据集的内容，下面先将前两个数据点转成黑白图像显示出来。此外，把每个数据集都按 8:2 的比例随机划分成训练集（training set）和测试集（test set）。我们先在训练集上应用 KNN 算法，再在测试集上测试算法的表现。关于将数据集划分为训练集和测试集的原因，本书会在第 5 章中详细讲解。

本节中，我们会用到 NumPy 和 Matplotlib 两个 Python 库。NumPy 是科学计算库，包含了大量常用的计算工具，如数组工具、数据统计、线性代数等，我们用 NumPy 中的数组来存储数据，并且会用到其中的许多函数。Matplotlib 是可视化库，包含了各种绘图工具，我们用 Matplotlib 进行数据可视化，以及绘制各种训练结果。本书不会对库中该函数的用法做过多详细说明，感兴趣的读者可以自行查阅官方文档、API 或其他教程，了解相关函数的具体使用方法。

import matplotlib.pyplot as plt
import numpy as np
import os


# 读入mnist数据集
m_x = np.loadtxt('mnist_x', delimiter=' ')
m_y = np.loadtxt('mnist_y')


# 数据集可视化
data = np.reshape(np.array(m_x[0], dtype=int), [28, 28])
plt.figure()
plt.imshow(data, cmap='gray')


# 将数据集分为训练集和测试集
ratio = 0.8
split = int(len(m_x) * ratio)
# 打乱数据
np.random.seed(0)
idx = np.random.permutation(np.arange(len(m_x)))
m_x = m_x[idx]
m_y = m_y[idx]
x_train, x_test = m_x[:split], m_x[split:]
y_train, y_test = m_y[:split], m_y[split:]

png

下面是 KNN 算法的具体实现。首先，我们定义样本之间的距离。简单起见，我们采用最常用的欧氏距离（Euclidean distance），也就是我们最生活中最常用、最直观的空间距离。对于维空间中的两个点和，其欧氏距离为：

def distance(a, b):
    return np.sqrt(np.sum(np.square(a - b)))

为了方便，我们将 KNN 算法定义成类，其初始化参数是和类别的数量。每一部分的含义在代码中有详细注释。

class KNN:
    def __init__(self, k, label_num):
        self.k = k
        self.label_num = label_num # 类别的数量


    def fit(self, x_train, y_train):
        # 在类中保存训练数据
        self.x_train = x_train
        self.y_train = y_train


    def get_knn_indices(self, x):
        # 获取距离目标样本点最近的K个样本点的标签
        # 计算已知样本的距离
        dis = list(map(lambda a: distance(a, x), self.x_train))
        # 按距离从小到大排序，并得到对应的下标
        knn_indices = np.argsort(dis)
        # 取最近的K个
        knn_indices = knn_indices[:self.k]
        return knn_indices


    def get_label(self, x):
        # 对KNN方法的具体实现，观察K个近邻并使用np.argmax获取其中数量最多的类别
        knn_indices = self.get_knn_indices(x)
        # 类别计数
        label_statistic = np.zeros(shape=[self.label_num])
        for index in knn_indices:
            label = int(self.y_train[index])
            label_statistic[label] += 1
        # 返回数量最多的类别
        return np.argmax(label_statistic)


    def predict(self, x_test):
        # 预测样本 test_x 的类别
        predicted_test_labels = np.zeros(shape=[len(x_test)], dtype=int)
        for i, x in enumerate(x_test):
            predicted_test_labels[i] = self.get_label(x)
        return predicted_test_labels

最后，我们在测试集上观察算法的效果，并对不同的的取值进行测试。

for k in range(1, 10):
    knn = KNN(k, label_num=10)
    knn.fit(x_train, y_train)
    predicted_labels = knn.predict(x_test)


    accuracy = np.mean(predicted_labels == y_test)
    print(f'K的取值为 {k}, 预测准确率为 {accuracy * 100:.1f}%')
K的取值为 1, 预测准确率为 88.5%
K的取值为 2, 预测准确率为 88.0%
K的取值为 3, 预测准确率为 87.5%
K的取值为 4, 预测准确率为 87.5%
K的取值为 5, 预测准确率为 88.5%
K的取值为 6, 预测准确率为 88.5%
K的取值为 7, 预测准确率为 88.0%
K的取值为 8, 预测准确率为 87.0%
K的取值为 9, 预测准确率为 87.0%

3.3 使用 scikit-learn 实现 KNN 算法

Python 作为机器学习的常用工具，有许多 Python 库已经封装好了机器学习常用的各种算法。这些库通常经过了很多优化，其运行效率比上面我们自己实现的要高。所以，能够熟练掌握各种机器学习库的用法，也是机器学习的学习目标之一。其中，scikit-learn（简称 sklearn）是一个常用的机器学习算法库，包含了数据处理工具和许多简单的机器学习算法。本节以 sklearn 库为例，来讲解如何使用封装好的 KNN 算法，并在高斯数据集 gauss.csv 上观察分类效果。该数据集包含一些平面上的点，分别由两个独立的二维高斯分布随机生成，每一行包含三个数，依次是点的和坐标和类别。首先，我们导入数据集并进行可视化。

from sklearn.neighbors import KNeighborsClassifier # sklearn中的KNN分类器
from matplotlib.colors import ListedColormap


# 读入高斯数据集
data = np.loadtxt('gauss.csv', delimiter=',')
x_train = data[:, :2]
y_train = data[:, 2]
print('数据集大小：', len(x_train))


# 可视化
plt.figure()
plt.scatter(x_train[y_train == 0, 0], x_train[y_train == 0, 1], c='blue', marker='o')
plt.scatter(x_train[y_train == 1, 0], x_train[y_train == 1, 1], c='red', marker='x')
plt.xlabel('X axis')
plt.ylabel('Y axis')
plt.show()
数据集大小： 200

png

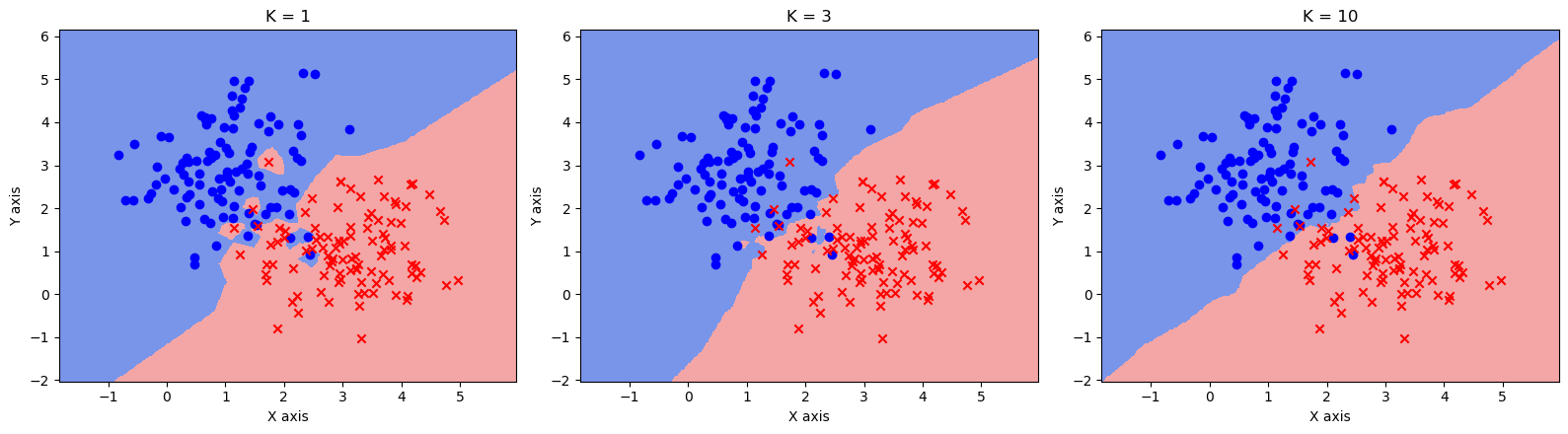
在高斯数据集中，我们将整个数据集作为训练集，将平面上的其他点作为测试集，观察 KNN 在不同的值下的分类效果。因此，我们不对数据集进行划分，而是在平面上以 0.02 为间距构造网格作为测试集。由于平面上的点是连续的，我们无法依次对它们测试，只能像这样从中采样。在没有特殊要求的情况下，我们一般采用最简单的均匀网格采样。这里，我们选用网格间距 0.02 是为了平衡测试点的个数和测试点的代表性，读者也可以调整该数值观察结果的变化。

# 设置步长
step = 0.02
# 设置网格边界
x_min, x_max = np.min(x_train[:, 0]) - 1, np.max(x_train[:, 0]) + 1
y_min, y_max = np.min(x_train[:, 1]) - 1, np.max(x_train[:, 1]) + 1
# 构造网格
xx, yy = np.meshgrid(np.arange(x_min, x_max, step), np.arange(y_min, y_max, step))
grid_data = np.concatenate([xx.reshape(-1, 1), yy.reshape(-1, 1)], axis=1)

在 sklearn 中，KNN 分类器由KNeighborsClassifier定义，通过参数n_neighbors指定的大小。我们分别设置，和观察分类效果。数据集中的点用深色表示，平面上被分到某一类的点用与其相对应的浅色表示。可以看出，随着的增大，分类的边界变得更平滑，但错分的概率也在变大。

fig = plt.figure(figsize=(16,4.5))
# K值，读者可以自行调整，观察分类结果的变化
ks = [1, 3, 10]
cmap_light = ListedColormap(['royalblue', 'lightcoral'])


for i, k in enumerate(ks):
    # 定义KNN分类器
    knn = KNeighborsClassifier(n_neighbors=k)
    knn.fit(x_train, y_train)
    z = knn.predict(grid_data)


    # 画出分类结果
    ax = fig.add_subplot(1, 3, i + 1)
    ax.pcolormesh(xx, yy, z.reshape(xx.shape), cmap=cmap_light, alpha=0.7)
    ax.scatter(x_train[y_train == 0, 0], x_train[y_train == 0, 1], c='blue', marker='o')
    ax.scatter(x_train[y_train == 1, 0], x_train[y_train == 1, 1], c='red', marker='x')


    ax.set_xlabel('X axis')
    ax.set_ylabel('Y axis')
    ax.set_title(f'K = {k}')
plt.show()

png

3.4 用 KNN 算法完成回归任务——色彩风格迁移

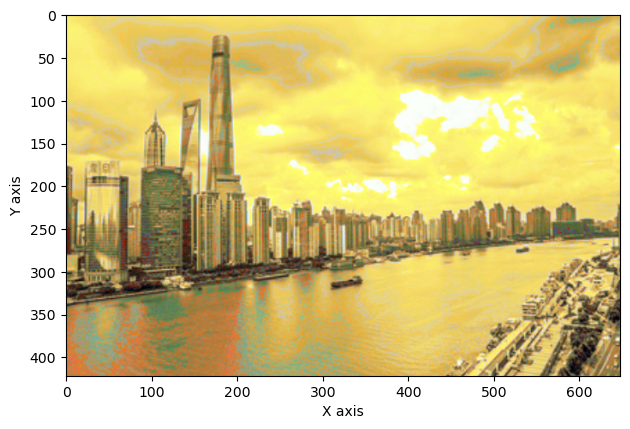
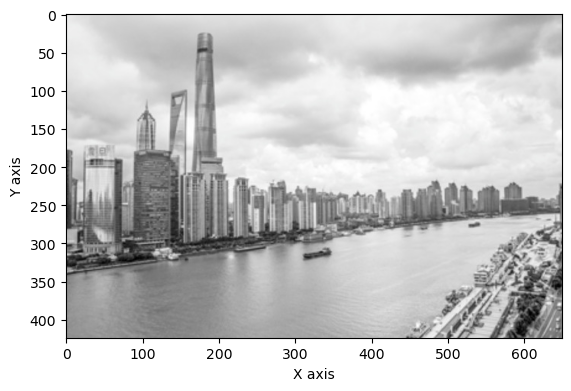
上面我们展示了 KNN 在分类任务上的效果，本节我们将 KNN 算法应用到回归任务——色彩风格迁移上。在该任务中，我们的目标是给一张黑白照片上色，同时要求上色的风格要接近另一张彩色照片。如图 3-2 所示，内容图像 A 是一张上海外滩的黑白风景照片，风格图像 B 是梵高著名的画作《星空》。通过色彩风格迁移，我们可以达到图像 C 中的上色效果。梵高作为著名的荷兰后印象派画家，其画作色彩比较夸张奔放，常常采用一些高明度、高纯度的色彩。得益于其富有特色的色彩，我们可以从风格迁移中明显观察到图像风格的转变。因此，在后续任务中，我们都采用这张外滩风景作为内容图像，而用梵高的不同作品当做风格图像。

transfer
图 3-2 任务图像展示

首先，我们安装导入必要的库。本节会用到 scikit-image（简称 skimage）这一图像处理库，以及 sklearn 中的 KNN 回归器KNeighborsRegressor。

!pip install scikit-image
from skimage import io # 图像输入输出
from skimage.color import rgb2lab, lab2rgb # 图像通道转换
from sklearn.neighbors import KNeighborsRegressor # KNN 回归器
import os


path = 'style_transfer'
Requirement already satisfied: scikit-image in f:\anaconda3\lib\site-packages (0.19.2)
Requirement already satisfied: imageio>=2.4.1 in f:\anaconda3\lib\site-packages (from scikit-image) (2.19.3)
Requirement already satisfied: pillow!=7.1.0,!=7.1.1,!=8.3.0,>=6.1.0 in f:\anaconda3\lib\site-packages (from scikit-image) (9.2.0)
Requirement already satisfied: tifffile>=2019.7.26 in f:\anaconda3\lib\site-packages (from scikit-image) (2021.7.2)
Requirement already satisfied: packaging>=20.0 in f:\anaconda3\lib\site-packages (from scikit-image) (21.3)
Requirement already satisfied: PyWavelets>=1.1.1 in f:\anaconda3\lib\site-packages (from scikit-image) (1.3.0)
Requirement already satisfied: scipy>=1.4.1 in f:\anaconda3\lib\site-packages (from scikit-image) (1.9.1)
Requirement already satisfied: numpy>=1.17.0 in f:\anaconda3\lib\site-packages (from scikit-image) (1.21.5)
Requirement already satisfied: networkx>=2.2 in f:\anaconda3\lib\site-packages (from scikit-image) (2.8.4)
Requirement already satisfied: pyparsing!=3.0.5,>=2.0.2 in f:\anaconda3\lib\site-packages (from packaging>=20.0->scikit-image) (3.0.9)




WARNING: There was an error checking the latest version of pip.

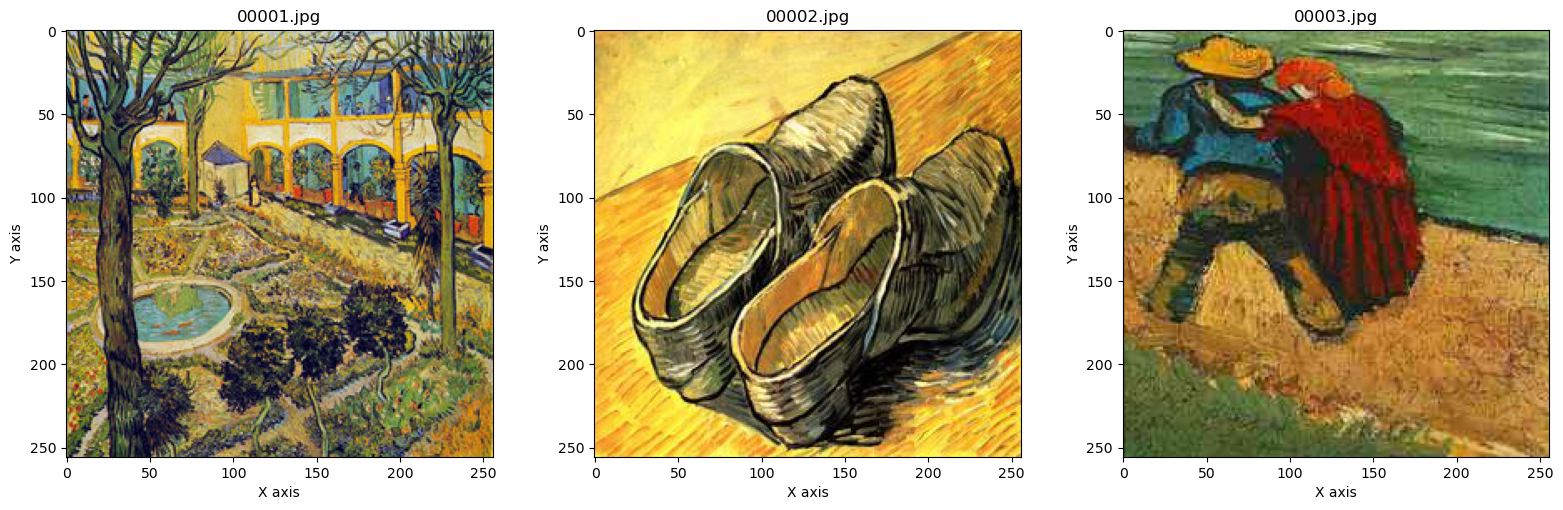
在讲解 KNN 的用法之前，我们必须要了解如何表示图像的色彩。我们先将部分用到的梵高画作展示出来，让读者有较为清晰的感受。数据集中，每幅画作都由 256256 个像素来表示。

data_dir = os.path.join(path, 'vangogh')
fig = plt.figure(figsize=(16, 5))
for i, file in enumerate(np.sort(os.listdir(data_dir))[:3]):
    img = io.imread(os.path.join(data_dir, file))
    ax = fig.add_subplot(1, 3, i + 1)
    ax.imshow(img)
    ax.set_xlabel('X axis')
    ax.set_ylabel('Y axis')
    ax.set_title(file)
plt.show()

png

3.4.1 RGB 空间与 LAB 空间

我们知道，所有颜色都可以由三原色红、绿、蓝混合得到。因此，在计算机中，为了表示图像中每个像素的颜色，我们常用 RGB 表示法。其中 R（red）、G（green）和 B（blue）分别代表红、绿、蓝在颜色中所占的比例，均为 0~255 间的整数。将整张图像上每个像素的 RGB 值分别合在一起，就得到了如图 3-3 所示的图像的 RGB 矩阵。如果图像的高是，宽是，这一的矩阵就包含了图像的色彩信息。

rgb
图 3-3 RGB空间示意

然而，RGB 表示法中对数字大小的限制使得 RGB 并不能表示出所有颜色。除了 RGB 之外，计算机中还常用 LAB 法来表示颜色。其中，L（light）代表亮度，A 表示红、绿方向的分量，B 表示黄、蓝方向的分量。虽然 LAB 理论上也能表示所有颜色，但由于实际应用中的限制，一般规定 L 的范围是 0~100，0 代表黑色，100 代表白色；A 为-128~127，负数代表绿色，正数代表红色；B 也为-128~127，负数代表蓝色，正数代表黄色。图 3-4 展示了 LAB 空间的色彩变化。相比于 RGB，LAB 将亮度信息提取出来，与色彩信息独立，使我们可以在不改变黑白图像亮度的情况下对其上色，完成色彩风格迁移。

lab
图 3-4 LAB空间示意

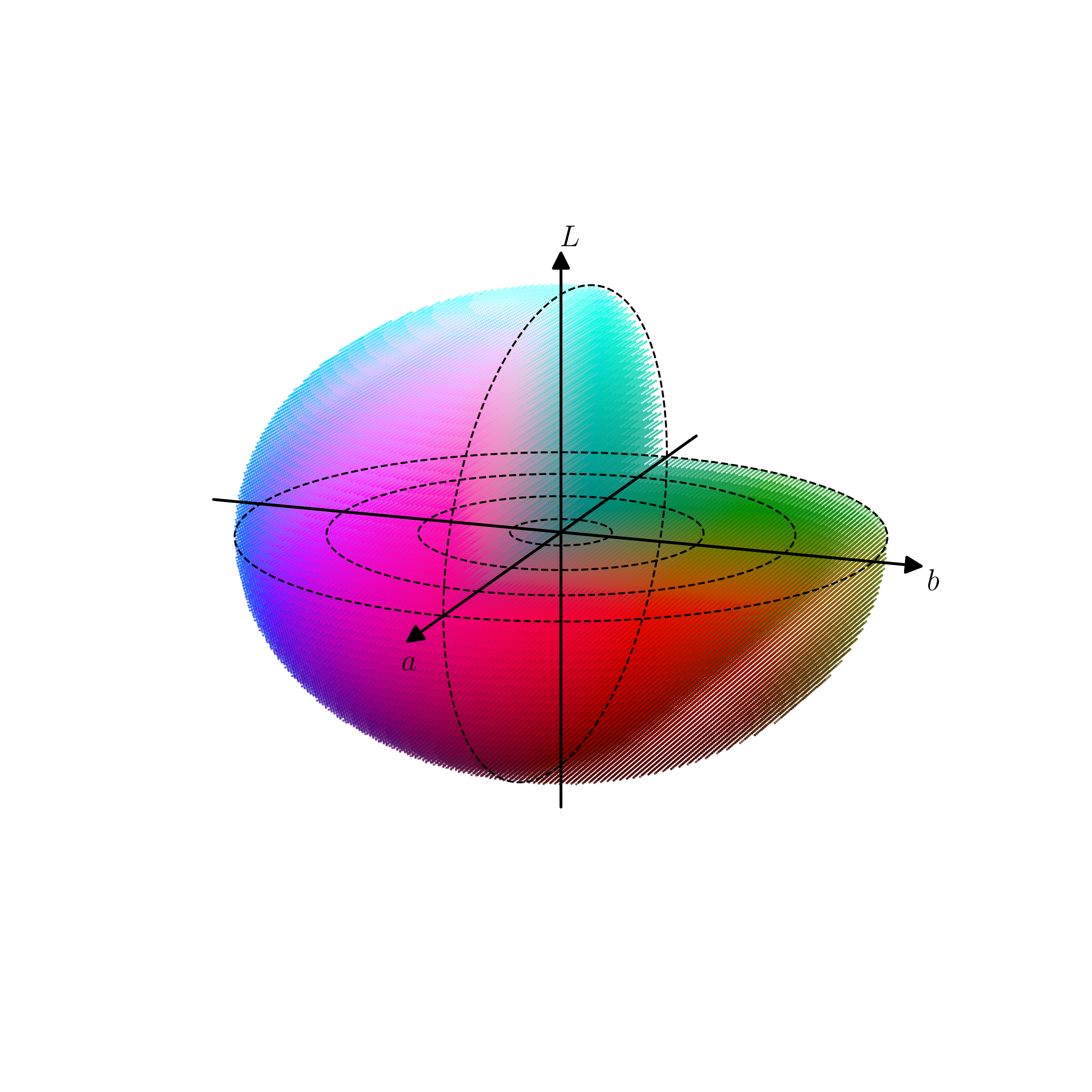
3.4.2 算法设计

在确定了图像色彩的表示方式后，上色的过程就是确立从黑白图像到彩色图像的颜色映射的过程。然而，黑白图像中只有亮度信息，我们无法直接还原出其对应的颜色。因此，需要为其补充额外的信息。我们可以采用 KNN 算法来完成这一映射。首先，我们将风格图像也变成黑白的，提取出其灰度信息。接下来，最简单的思路是，将内容图像中的像素到黑白风格图像中进行匹配，用最接近的个像素的原始颜色取平均，作为该像素上色后的颜色。

然而，这一想法所利用到的信息太少，最后上色的效果也不佳。在内容图像中，同样的灰度像素既可能出现在黄色的土地上，也可能出现在蓝色的天上。如果将这些差异很大的颜色取平均进行上色，自然得不到我们期望的效果。就像在一个人组成的方阵中，只靠身高去找人一样。同样身高的人可能有很多，我们很难准确定位要找的人。但是，如果我们又知道了目标周围相邻的人的身高，就可以大大提高精确度。因此，我们将匹配的范围扩大，对于内容图像中的任意一个像素点，我们取其周围相邻的 8 个像素，组成 33的窗口，再向黑白风格图像中寻找与其最相似的个33 的像素窗口。最后，把这些窗口的中心像素的颜色取平均，作为该像素的颜色。图 3-5 描述了上述使用 KNN 算法的思路。

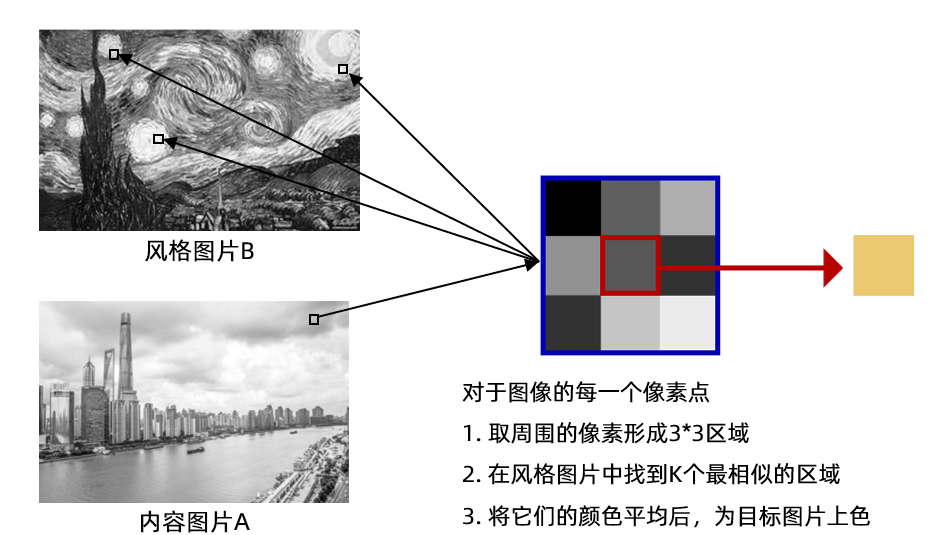
knn_transfer
图 3-5 用KNN解决色彩迁移问题的算法

下面，我们就来实现这一算法。首先记录风格图像中每个窗口对应的原始颜色，供最后上色使用。

# block_size表示向外扩展的层数，扩展1层即3*3
block_size = 1


def read_style_image(file_name, size=block_size):
    # 读入风格图像, 得到映射 X->Y
    # 其中X储存3*3像素格的灰度值，Y储存中心像素格的色彩值
    # 读取图像文件，设图像宽为W，高为H，得到W*H*3的RGB矩阵
    img = io.imread(file_name)
    fig = plt.figure()
    plt.imshow(img)
    plt.xlabel('X axis')
    plt.ylabel('Y axis')
    plt.show()


    # 将RGB矩阵转换成LAB表示法的矩阵，大小仍然是W*H*3，三维分别是L、A、B
    img = rgb2lab(img)
    # 取出图像的宽度和高度
    w, h = img.shape[:2]


    X = []
    Y = []
    # 枚举全部可能的中心点
    for x in range(size, w - size):
        for y in range(size, h - size):
            # 保存所有窗口
            X.append(img[x - size: x + size + 1, \
                y - size: y + size + 1, 0].flatten())
            # 保存窗口对应的色彩值a和b
            Y.append(img[x, y, 1:])
    return X, Y

接下来，读取梵高的《星空》作为风格图像，并用 sklearn 中的 KNN 回归器建立模型。

X, Y = read_style_image(os.path.join(path, 'style.jpg')) # 建立映射


# weights='distance'表示邻居的权重与其到样本的距离成反比
knn = KNeighborsRegressor(n_neighbors=4, weights='distance')
knn.fit(X, Y)

png

KNeighborsRegressor(n_neighbors=4, weights='distance')

我们将内容图像分割成同样大小的窗口，并用 KNN 模型上色。

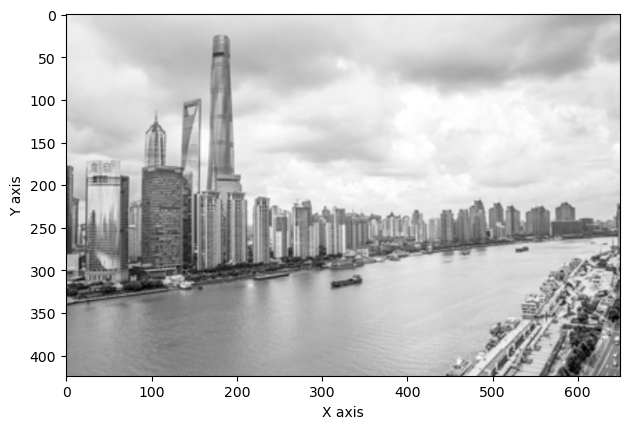
def rebuild(img, size=block_size):
    # 打印内容图像
    fig = plt.figure()
    plt.imshow(img)
    plt.xlabel('X axis')
    plt.ylabel('Y axis')
    plt.show()


    # 将内容图像转为LAB表示
    img = rgb2lab(img)
    w, h = img.shape[:2]


    # 初始化输出图像对应的矩阵
    photo = np.zeros([w, h, 3])
    # 枚举内容图像的中心点，保存所有窗口
    print('Constructing window...')
    X = []
    for x in range(size, w - size):
        for y in range(size, h - size):
            # 得到中心点对应的窗口
            window = img[x - size: x + size + 1, \
                y - size: y + size + 1, 0].flatten()
            X.append(window)
    X = np.array(X)


    # 用KNN回归器预测颜色
    print('Predicting...')
    pred_ab = knn.predict(X).reshape(w - 2 * size, h - 2 * size, -1)
    # 设置输出图像
    photo[:, :, 0] = img[:, :, 0]
    photo[size: w - size, size: h - size, 1:] = pred_ab


    # 由于最外面size层无法构造窗口，简单起见，我们直接把这些像素裁剪掉
    photo = photo[size: w - size, size: h - size, :]
    return photo

最后，我们设置相关参数，并展示风格迁移后的图像。

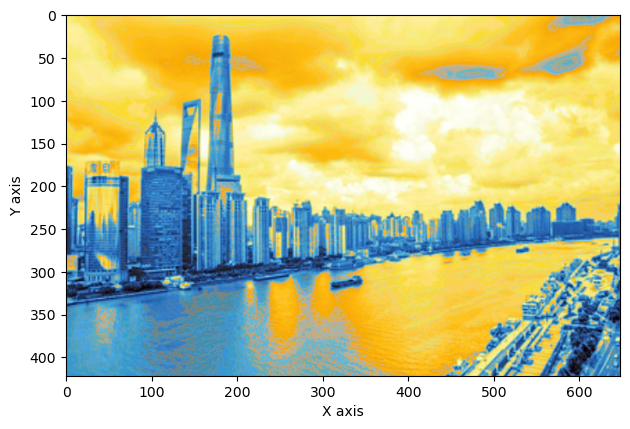
content = io.imread(os.path.join(path, 'input.jpg'))
new_photo = rebuild(content)
# 为了展示图像，我们将其再转换为RGB表示
new_photo = lab2rgb(new_photo)


fig = plt.figure()
plt.imshow(new_photo)
plt.xlabel('X axis')
plt.ylabel('Y axis')
plt.show()

png

Constructing window...
Predicting...

png

3.5 本章小结

本章主要讲述了 KNN 算法的原理，并在分类和回归任务上进行了应用。KNN 算法作为最简单的机器学习算法之一，其统计的思想仍然在多个领域中有着广泛应用。此外，机器学习的各种工具库也是机器学习必不可少的一部分。读者在学习理论的同时，也应当多动手实践，观察不同参数等带来的影响。

习题

  1. 在 KNN 算法中，我们将训练集上的平方误差和作为选择的标准，是否正确？ A. 错误 B. 正确

  2. 关于 KNN 算法描述错误的是： A. KNN 算法用于分类和回归问题。 B. KNN 算法在空间中找到个最接近的样本进行预测。 C. KNN 算法的是经过学习得到的。

  3. 本节的 KNN 算法中，我们采用了最常用的欧氏距离作为寻找邻居的标准。在哪些场景下，我们可能会用到其他距离度量，例如曼哈顿距离（Manhattan distance）？把第 3 节实验中的距离改为曼哈顿距离，观察对分类效果的影响。

  4. 在色彩风格迁移中，如果扩大采样的窗口，可能会产生什么问题？调整窗口大小并观察结果。

  5. 思考一下自己在生活、工作中，是否也使过 KNN 算法？自己为什么使用 KNN 算法来处理碰到的问题？

  6. 在本书的在线版本里，我们在 vangogh 文件夹下还提供了许多其他的梵高画作。如果我们将所有画作中的窗口都提取出来，用 KNN 去匹配，最后上色的结果会是什么样？下面提供了相关代码，观察结果，并思考产生该结果的原因。从中可以发现，当使用 KNN 解决问题时，需要注意什么？

# 创建由多张图像构成的数据集，num表示图像数量
# 返回的X、Y的含义与函数read_style_image相同
def create_dataset(data_dir='vangogh', num=10):
    # 初始化函数输出
    X = []
    Y = []
    # 读取图像
    files = np.sort(os.listdir(os.path.join(path, data_dir)))
    num = min(num, len(files))
    for file in files[:num]:
        print('reading', file)
        X0, Y0 = read_style_image(os.path.join(path, data_dir, file))
        X.extend(X0)
        Y.extend(Y0)
    return X, Y


X, Y = create_dataset()
knn = KNeighborsRegressor(n_neighbors=4, weights='distance')
knn.fit(X, Y)


content = io.imread(os.path.join(path, 'input.jpg'))
new_photo = rebuild(content)
new_photo = lab2rgb(new_photo)


fig = plt.figure()
plt.imshow(new_photo)
plt.xlabel('X axis')
plt.ylabel('Y axis')
plt.show()
reading 00001.jpg

png

reading 00002.jpg

png

reading 00003.jpg

png

reading 00004.jpg

png

reading 00005.jpg

png

reading 00006.jpg

png

reading 00007.jpg

png

reading 00008.jpg

png

reading 00009.jpg

png

reading 00010.jpg

png

png

Constructing window...
Predicting...

png

2023/9/13 16:27:41