第 17 章 EM算法

本章我们继续介绍概率相关模型的算法。在前面的章节中，我们已经讲解了贝叶斯网络与最大似然估计（MLE）。对于监督学习的任务，设数据集的样本为，标签为，我们用和分别表示全体样本和全体标签。那么，我们可以通过最大化对数似然来求解模型的参数。而对于无监督学习任务，我们要求解样本的分布。这时，我们通常需要先假设数据服从某种分布，再求解这个分布的参数。例如假设数据呈现高斯分布，然后可以通过 MLE 的方式来求得最佳的高斯分布参数和。

更进一步思考，真实世界的数据分布往往较为复杂，其背后往往具有一定的结构性，直接使用一个概率分布模型无法有效刻画数据分布。例如，我们可以假设数据服从高斯混合模型（Gaussian mixture model，GMM），该模型是由个相互独立的高斯分布组合而成的，数据集中的每个样本都从其中的某个高斯分布采样得到。在现实生活中，符合GMM的数据集有很多。例如，我们统计了某学校中所有学生的身高。通常认为，人的身高是在某个均值附近的高斯分布，然而男生和女生身高的均值是不同的。因此，我们可以认为男生身高和女生身高分别服从不同的高斯分布，而总的数据集就符合GMM。

在GMM中，我们要求解的参数共有两种，一种是每个高斯分布的参数和，另一种是每个高斯分布在GMM中的占比。记是高斯分布的编号，出现的次数越多，从分布采样的数据在数据集中的占比就越大。所以，后者相当于求解的多项分布。

从贝叶斯网络的角度来看，上面的分析过程建立了如下图所示的贝叶斯网络。其中，是多项分布的参数，取的概率分别是。而对每个样本，我们先从多项分布中采样，确定样本属于哪个高斯分布，再从该高斯分布中采样出样本。于是，我们可以利用中间变量把的分布拆分为。

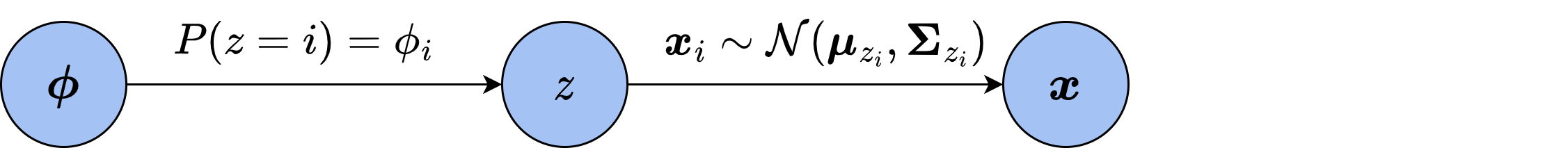
按照MLE的思想，参数的似然就是在此参数条件下出现观测到的数据分布的概率，也即。我们将似然取对数，得到：

为了求出使对数似然最大化的参数，我们需要令对数似然对3个参数的梯度均为零：

然而，上述方程的求解非常复杂，并且没有解析解。因此，我们需要寻找其他方法求解。本章介绍的EM算法是一种求解复杂分布参数的通用算法。

17.1 高斯混合模型的EM算法

我们在最开始为了拆分的分布引入了中间变量，用来指示每个样本属于哪个高斯分布，而的分布就是混合高斯分布中每个分布的占比。像这样虽然不能直接被观测到、但是可以直接影响最后观测结果的变量，就称为隐变量（latent variable）。通常来说，隐变量比可观测的变量更本质。因此，我们经常会用引入隐变量的方法来把复杂的问题简单化。同时，隐变量也对问题的求解有关键作用。在对数似然的表达式中，如果每个样本所属的高斯分布编号已知，那么推导的倒数第二步中一项在时就变为。因此，对数似然可以写为：

求这一函数的最大值就相对容易了。首先，由于已知，其多项分布的参数可以直接通过统计数据集中属于每个高斯分布的样本比例得到：

这里，表示数据集中属于第个高斯分布的样本数目。每个高斯分布之间的参数是相互独立的，并且在已知的条件下，它们也和独立。这一点从上面的贝叶斯网络示意图中也可以看出来，当中间的节点已知时，左右两端的节点之间不存在依赖关系。高斯分布的参数分别是均值和协方差，也可以从数据集中属于该分布的样本直接计算出来：

求和中每一项的因子是为了筛选出属于第个高斯分布的样本。如果样本不属于分布，那么这一项就为0，对求和没有贡献。如果我们已知的是隐变量的分布，也即第个样本属于第个高斯分布的概率是，那么上面的计算公式也相应的改为：

反过来考虑，如果我们已经知道了分布的参数，我们同样也可以推断出每个样本属于第个高斯分布的概率。根据贝叶斯公式可以得到的后验分布为：

在各个参数已知的情况下，分子分母都可以直接计算出来。到此为止，看起来我们似乎在进行循环论证，在已知的前提下可以计算出参数，而在已知参数的前提下可以计算出，但是这两者都是未知的。因此，我们可以采用之前用过许多次的近似方式，先固定其中一方来优化另一方，再反过来固定另一方，如此迭代，这就形成了EM算法的基本思想。具体在本例中，EM算法每一次迭代由两步构成：

1. 期望步骤（E-step）：固定各个参数，由数据集中的样本统计计算隐变量的后验分布。

2. 最大化步骤（M-step）：固定隐变量，最大化参数的对数似然。

由于两步分别在计算样本的统计期望和最大化参数的对数似然，这样交替优化隐变量和参数的方法就称为期望-最大化算法，简称EM算法。

17.2 动手求解GMM拟合数据分布

虽然GMM是由高斯分布组成的，然而理论上它可以用来拟合任意的数据分布。如图17-2所示，左上角是由加上随机的高斯噪声生成的数据，显然这些数据并不符合高斯分布。如果我们试图用两个高斯分布来拟合数据，如右上角所示，每个椭圆形区域表示拟合出的一个高斯分布，可以看出该结果与实际数据偏差仍然较大。但是，当我们继续增加GMM中高斯分布的数目时，拟合结果也会越来越精确。下图的左下方和右下方分别展示了用5个和10个高斯分布拟合出的结果，已经可以基本覆盖所有的数据点，且几乎没有多出的区域。事实上我们可以证明，任何数据分布都可以用GMM来无限逼近。而在现实场景中，由于高斯分布简单易算、性质良好，GMM也就成为了最常用的模型之一。

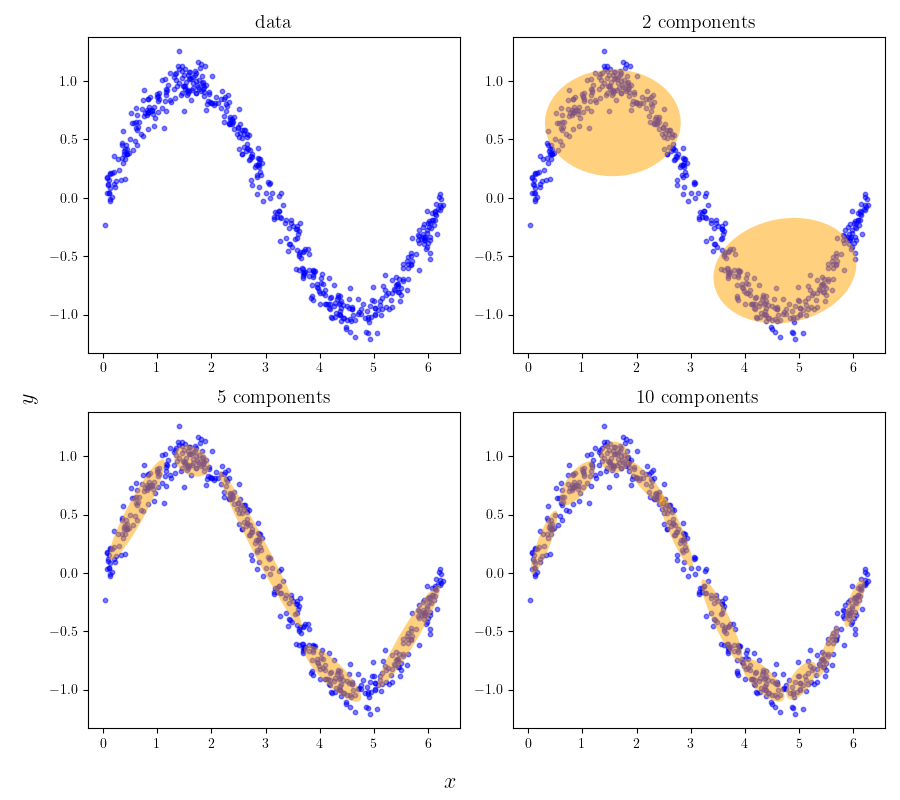
从上图的拟合结果中我们还可以发现，如果我们有一组分布未知的数据，并且还希望能按照同样的分布生成一些新的数据，那么也可以先用GMM对数据进行拟合，再由它来继续做数据生成。因此，从数据中拟合GMM就变得十分重要。下面，我们就来用上文介绍的EM算法来求解GMM模型。简单起见，我们就采用与上图中相同的正弦数据集。

import numpy as np
import matplotlib.pyplot as plt

X = np.loadtxt('sindata.csv', delimiter=',')

在实现EM算法之前，我们先来定义计算高斯分布概率密度的函数。设，那么概率密度的表达式为：

式中，表示矩阵的行列式，可以用numpy.linalg中的工具直接计算得到。此外，我们通常会计算概率密度的对数而非概率密度本身，这是因为形如的式子在计算时，前面的对数-求和-指数部分可以进行优化，其速度相对更快。如果我们计算的是，就可以将对数似然计算中的第二个求和转化为对数-求和-指数的形式。

# 计算多元高斯分布的概率密度的对数
def log_gaussian_prob(x, mu, sigma):
    d = x.shape[-1]
    det = np.linalg.det(sigma)
    diff = x - mu
    # 由于x可能包含多个样本
    # x.T @ inv(sigma) @ x 的第二个乘法只需要保留前后样本一致的部分，
    # 所以第二个乘法用点乘再求和代替
    # 此外，由于数据存储维度的问题，这里的转置和上面公式中的转置相反
    log_prob = -d / 2 * np.log(2 * np.pi) - 0.5 * np.log(det) \
             - 0.5 * np.sum(diff @ np.linalg.inv(sigma) * diff, axis=-1)
    return log_prob

接下来是EM算法的核心部分。为了使算法的调用和参数设置尽可能灵活，我们把EM算法封装在GMM类中。上文中只介绍了EM算法的迭代过程，但没有提及该如何初始化算法的各个参数。为了使算法从比较良好的初始状态出发，我们可以用k-means算法先对数据做聚类，得到每个点的聚类标签。如果将每个聚类看成一个高斯分布，那么这就相当于计算出了每个样本属于哪个分布，也就是隐变量。最后，再从统计计算出每个分布的均值和协方差即可完成初始化。

下面的代码中，我们分别实现随机初始化和k-means初始化两种方法。需要注意，协方差矩阵必须是半正定的，因此我们先在范围内均匀采样矩阵的每个元素，再加上倍的单位矩阵，从而保证矩阵的半正定性。

from sklearn.cluster import KMeans
from scipy.special import logsumexp

class GMM:

    def __init__(self, n_components=2, eps=1e-4, max_iter=100, init='random'):
        # n_components：GMM中高斯分布的数目
        # eps：迭代精度，当对数似然的变化小于eps时迭代终止
        # max_iter：最大迭代次数
        # init：初始化方法，random或kmeans
        self.k = n_components
        self.eps = eps
        self.max_iter = max_iter
        self.init = init
        self.phi = None # 隐变量的先验分布，即每个高斯分布的占比
        self.means = None # 每个高斯分布的均值
        self.covs = None # 每个高斯分布的协方差

    def EM_fit(self, X):
        # 用EM算法求解GMM的参数
        # 参数初始化
        if self.init == 'random': 
            self._random_init_params(X) 
        elif self.init == 'kmeans':
            self._kmeans_init_params(X)
        else:
            raise NotImplementedError
        ll = self._calc_log_likelihood(X) # 当前的对数似然
        n, d = X.shape
        # 开始迭代
        qz = np.zeros((n, self.k)) # z的后验分布
        for t in range(self.max_iter):
            # E步骤，更新后验分布
            for i in range(self.k):
                # 计算样本属于第i类的概率
                log_prob = log_gaussian_prob(X, self.means[i], self.covs[i])
                qz[:, i] = self.phi[i] * np.exp(log_prob)
            # 归一化
            qz = qz / np.sum(qz, axis=1).reshape(-1, 1)

            # M步骤，统计更新参数，最大化对数似然
            self.phi = np.sum(qz, axis=0) / n # 更新隐变量分布
            for i in range(self.k):
                # 更新均值
                self.means[i] = np.sum(qz[:, i, None] * X, axis=0) \
                    / n / self.phi[i]
                # 更新协方差
                diff = X - self.means[i]
                self.covs[i] = (qz[:, i, None] * diff).T @ diff \
                    / (n - 1) / self.phi[i]
            
            # 判断对数似然是否收敛
            new_ll = self._calc_log_likelihood(X)
            # assert new_ll >= ll, new_ll
            if new_ll - ll <= self.eps:
                break
            ll = new_ll
            
    def _calc_log_likelihood(self, X):
        # 计算当前的对数似然
        ll = 0
        for i in range(self.k):
            log_prob = log_gaussian_prob(X, self.means[i], self.covs[i])
            # 用logsumexp简化计算
            # 该函数底层对对数-求和-指数形式的运算做了优化
            ll += logsumexp(log_prob + np.log(self.phi[i]))
        return ll

    def _random_init_params(self, X):
        self.phi = np.random.uniform(0, 1, self.k) # 随机采样phi
        self.phi /= np.sum(self.phi)
        self.means = np.random.uniform(np.min(X), np.max(X), 
            (self.k, X.shape[1])) # 随机采样均值
        self.covs = np.random.uniform(-1, 1, 
            (self.k, X.shape[1], X.shape[1])) # 随机采样协方差
        self.covs += np.eye(X.shape[1]) * X.shape[1] # 加上维度倍的单位矩阵

    def _kmeans_init_params(self, X):
        # 用Kmeans算法初始化参数
        # 简单起见，我们直接调用sklearn库中的Kmeans方法
        kmeans = KMeans(n_clusters=self.k, init='random', 
            random_state=0).fit(X)
        # 计算高斯分布占比
        data_in_cls = np.bincount(kmeans.labels_, minlength=self.k)
        self.phi = data_in_cls / len(X)
        # 计算均值和协方差
        self.means = np.zeros((self.k, X.shape[1]))
        self.covs = np.zeros((self.k, X.shape[1], X.shape[1]))
        for i in range(self.k):
            # 取出属于第i类的样本
            X_i = X[kmeans.labels_ == i]
            self.means[i] = np.mean(X_i, axis=0)
            diff = X_i - self.means[i]
            self.covs[i] = diff.T @ diff / (len(X_i) - 1)

最后，我们设置好超参数，用GMM模型拟合正弦数据集，并绘图观察拟合效果。由于绘图过程要用到从协方差矩阵计算椭圆参数、用matplotlib中的工具绘制椭圆等方法，较为复杂，我们在这里直接给出绘制椭圆的函数和使用方法，不再具体讲解绘制过程。我们分别用2、3、5、10个高斯分布和两种初始化方法进行拟合，并把结果画在一起进行对比。

import matplotlib as mpl

def plot_elipses(gmm, ax):
    # 绘制椭圆
    # gmm：GMM模型
    # ax：matplotlib的画布
    covs = gmm.covs
    for i in range(len(covs)):
        # 计算椭圆参数
        cov = covs[i][:2, :2]
        v, w = np.linalg.eigh(cov)
        u = w[0] / np.linalg.norm(w[0])
        ang = np.arctan2(u[1], u[0])
        ang = ang * 180 / np.pi
        v = 2.0 * np.sqrt(2.0) * np.sqrt(v)
        # 设置椭圆的绘制参数
        # facecolor和edgecolor分别是填充颜色和边缘颜色
        # 可以自由调整
        elp = mpl.patches.Ellipse(gmm.means[i, :2], v[0], v[1], 
            180 + ang, facecolor='orange', edgecolor='none')
        elp.set_clip_box(ax.bbox)
        # 设置透明度
        elp.set_alpha(0.5)
        ax.add_artist(elp)

# 超参数
max_iter = 100
eps = 1e-4
np.random.seed(0)

n_components = [2, 3, 5, 10]
inits = ['random', 'kmeans']
fig = plt.figure(figsize=(13, 25))
for i in range(8):
    ax = fig.add_subplot(4, 2, i + 1)
    # 绘制原本的数据点
    ax.scatter(X[:, 0], X[:, 1], color='blue', s=10, alpha=0.5)
    # 初始化并拟合GMM
    k = n_components[i // 2]
    init = inits[i % 2]
    gmm = GMM(k, eps, max_iter, init)
    gmm.EM_fit(X)
    # 绘制椭圆
    plot_elipses(gmm, ax)
    ax.set_title(f'{k} components, {init} init')
plt.show()

​
​

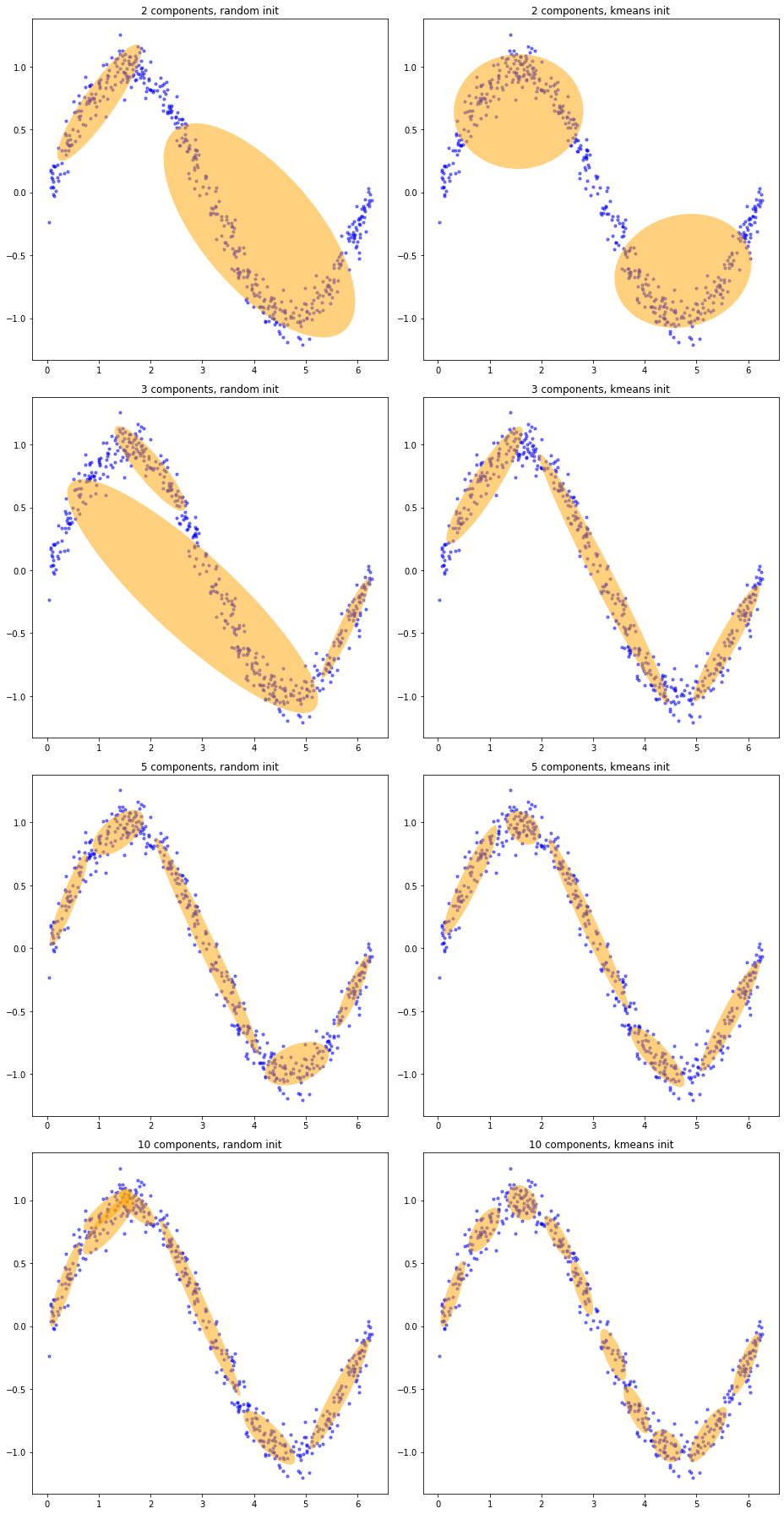
从结果图中可以看出，用k-means初始化参数可以让初始的聚类中心比较接近最优的高斯分布均值，而随机初始化的参数则很容易陷入局部的驻点。虽然EM算法理论上是收敛的，但是它并不保证收敛到最优解。并且，如果我们设置了对数似然的变化精度为算法的终止条件，那么算法同样可能在变化较为缓慢的驻点出停止，得到较差的解。因此，EM算法的参数初始化同样重要。除了k-means之外，我们还可以用随机性更小、效果更好的k-means++算法进行初始化，这部分代码留作习题，请读者自行完成。

小故事： GMM通常用来拟合数据分布后，再生成相同分布的数据。像这样从数据中学习出分布、再从分布出发完成后续任务的模型称为生成模型（generative model）。与之相对，直接学习样本特征和样本标签直接关联的模型称为判别模型（discriminative model）。我们之前介绍的线性回归等有监督学习模型都属于判别模型。从概率分布的角度出发，假设训练样本为，判别模型会将与关联起来，直接学习由样本给出标签的条件概率分布；而生成模型将所有样本关联起来，学习了联合分布，然后由此构建对其中标签的条件概率分布。在无监督学习下，生成模型只需要学习即可。

现代深度学习中，生成模型同样有广泛的应用。2013年，迪德里克·金玛（Diederik Kingma）和 马克斯·韦林（Max Welling）提出了变分自编码器；2014年，伊恩·古德费洛（Ian Goodfellow）提出了划时代的生成对抗网络。这两类模型衍生出了许多算法，让生成模型在深度学习时代保有了自己的一席之地。如今，最新的扩散模型在图像任务上取得了令人震惊的效果，并催生了足以以假乱真的人工智能绘画。用于文本任务的生成式预训练变换器可以生成高质量的自然语言，以它为基础的ChatGPT掀起了新一轮人工智能热潮。

17.3 一般情况下的EM算法

对于更一般的、样本分布不服从GMM的情况，我们同样可以模仿上面的步骤使用EM算法推进学习。设样本为，隐变量为，样本服从参数为的某个分布，那么参数的对数似然为：

上式的第二个求和是对隐变量的所有可能取值求和。如果隐变量连续，这里的求和应当改为积分。当每个样本的隐变量给定时，上式对的所有可能性求和就只剩下一项：

其中，表示样本对应的隐变量的值。

然而到此为止，我们并没有论证为什么EM算法是合理的。为什么可以假设隐变量已知？这样的迭代方式为何能给出收敛的结果？为了探究这一问题，我们来从头考虑MLE的求解。我们不妨先对原本的进行放缩，尝试求出其下界。设对每个样本，隐变量的分布是，满足归一性和非负性。这样对数似然可以写为：

为了进行放缩，我们介绍一个重要的常用不等式：琴生不等式（Jensen's inequality）。设函数是凸函数，那么任取自变量和，都有。反之，如果函数是凹函数，那么任取自变量和，都有。如果是严格凸或凹函数，那么上式的不等号在时严格成立，当且仅当时，等号成立。

下图以的图像为例展示了琴生不等式的含义。从图中可以看出，如果是凹函数，那么在图像上任意取两点连线，必定在函数曲线的下方。因此，自变量的组合所对应的函数值要高于函数值的组合。

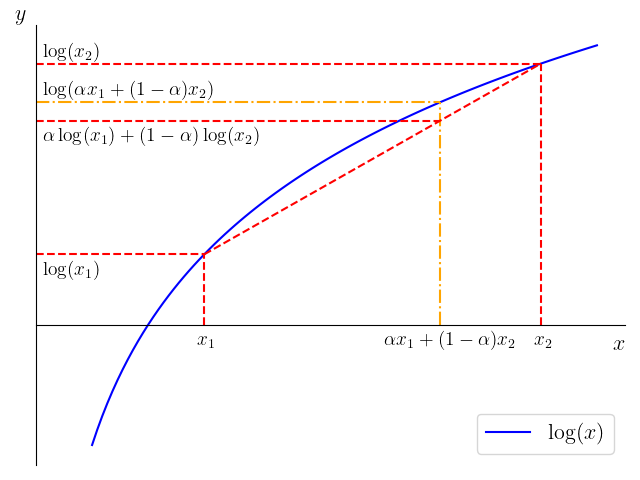
琴生不等式还可以推广到多个点的情况。设是凹函数，任取及其组合系数，且组合系数满足，那么：

注意到在上面对数似然的表达式中，是凹函数，内部求和的系数之和为1，于是由琴生不等式可得：

上式给出了对数似然的下界。虽然最大化较为困难，但是如果我们能提升其下界，就能为的值提供最低保证。如果下界不断提升，那么最后的就很可能接近其真正的最大值。因此，我们需要设法选取合适的，使其下界尽可能大。从琴生不等式的形式中容易看出，如果，不等式显然可以取到等号。而在下界的表达式中，相当于自变量，为了使等号成立，我们令：

其中是常数。这样，所有的“自变量”都等于，不等式等号成立。而常数可以由归一化条件得到。所以，的表达式为：

恰好是隐变量的后验分布。这也就解释了为什么EM算法的E步骤要计算的后验，再用后验分布得出的来优化。本质上，E步骤通过计算后验得出了的一个最好的下界，而M步骤通过调整参数来优化这一下界。而当M步一旦调整了参数，那么当前的下界就不再贴合而是严格小于，则又需要再次做E步骤，计算的后验，如此往复。那么这样的迭代是否保证能收敛呢？答案是肯定的，我们在下一节具体讨论EM算法的收敛性。

17.4 EM算法的收敛性

上一节中，我们通过放缩解释了EM算法的含义以及合理性，本节来继续证明算法的收敛性。由于我们最终要求解的是参数，记迭代第步的M步骤优化前参数为，那么我们需要证明优化后的参数会使对数似然函数增大，即。由于对数似然函数是一些不超过1的概率相乘再取对数，其上界为0，因此证明其单调递增就可以保证其收敛。同时，记第步隐变量的分布为，上面已经证明过，这一选择可以使琴生不等式取到等号。

证明的关键在于，注意到并不是参数对应的最优选择，从而