第 15 章 主成分分析

在上一章k均值聚类中，我们介绍了无监督学习的重要问题之一：聚类问题。结尾处我们提到，在解决复杂聚类问题时，第一步通常不会直接使用k均值算法，而是会先用其他手段提取数据的有用特征。对于高维复杂数据来说，其不同维度代表的特征可能存在关联，还有可能存在无意义的噪声干扰。因此，无论后续任务是有监督学习还是无监督学习，我们都希望能先从中提取出具有代表性、能最大限度保留数据本身信息的几个特征，从而降低数据维度，简化之后的分析和计算。这一过程通常称为数据降维（dimensionality reduction），同样是无监督学习中的重要问题。本章就来介绍数据降维中最经典的算法主成分分析（principal component analysis，PCA）。

15.1 主成分与方差

顾名思义，PCA的含义是将高维数据中的主要成分找出来。设原始数据，其中。我们的目标是通过某种变换，将数据的维度从减小到，且通常。变换后的数据不同维度之间线性无关，这些维度就称为主成分。也就是说，如果将变换后的数据排成矩阵，其中，那么的列向量是线性无关的。从矩阵的知识可以立即得到。

PCA算法不仅希望变换后的数据特征线性无关，更要求这些特征之间相互独立，也即任意两个不同特征之间的协方差为零。因此，PCA算法在计算数据的主成分时，会从第一个主成分开始依次计算，并保证每个主成分与之前的所有主成分都是正交的，直到选取了预先设定的个主成分为止。关于主成分选取的规则，我们以一个平面上的二元高斯分布为例来具体说明。如图15-1（a）所示，数据点服从以为中心、方向方差为1.5、方向方差为0.5、协方差为的二元高斯分布。从图中可以明显看出，当前的和两个特征之间存在关联，并不是独立的。

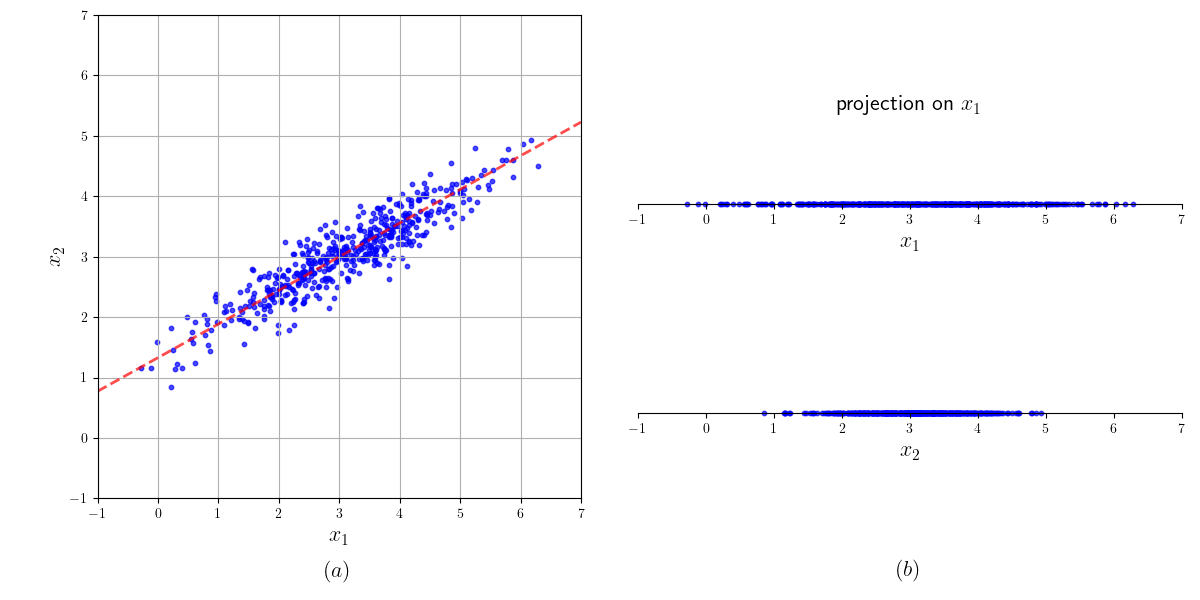
图15-1（b）展示了数据分别向和方向投影的结果。由于方向方差更大，数据在该方向的投影分布也更广。也就是说，数据向方向的投影保留了更多信息，是一个比更好的特征。如果我们不再把目光局限于和两个方向，而是考虑平面上的任意一个方向，那么如左图中红色虚线所示，沿直线的方向数据的方差是最大的，我们应当将此方向作为数据的特征之一。既然PCA算法希望选出的主成分保留最多的信息，那么就应当不断选取数据方差最大的方向作为主成分。因此，PCA计算的过程就是依次寻找方差最大方向的过程。

为了方便计算，我们通常要先对数据进行中心化，把当前每个特征都变为均值为0的分布。用表示数据的第个维度，那么均值为：

将数据中心化，得到：

以上面的高斯分布为例，变换后的图像如图15-2所示，其中心点已经从变为了。接下来在讨论时，我们默认数据都已经被中心化。下面，我们就来具体讲解如何寻找数据中方差最大的方向。

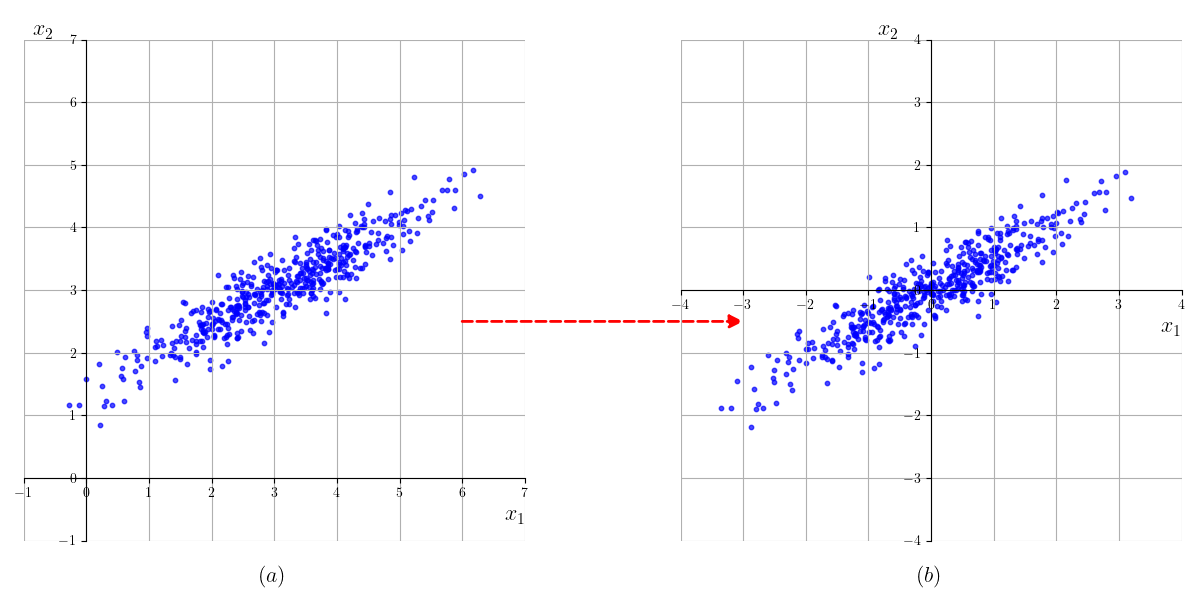
15.2 用特征分解计算PCA

为了找到方差最大的方向，我们先来计算样本在某个方向上的投影。设为方向向量，满足，向量在方向上的投影为。于是所有样本在方向上的方差为：

矩阵称为样本的协方差矩阵。由于是常数，简单起见，下面省略因子。要令方差最大，就相当于求解下面的优化问题：

在求解该问题之前，我们先来介绍矩阵的特征值（eigenvalue）与特征分解（eigendecomposition）相关的知识。对于方阵，如果向量与实数满足，就称是矩阵的特征值，为矩阵的特征向量。特征向量的任意非零实数倍满足

从而也还是特征向量。简单来说，矩阵作用到其特征向量上的结果等价于对该向量做伸缩变换，伸缩的倍数等于特征值，但不改变向量所在的直线。从这个角度来看，与共线，自然就是特征向量。因此，我们通常更关心单位特征向量，即长度为的特征向量。例如，矩阵

的特征值及其对应的单位特征向量有两组，分别为，和，，读者可以自行计算验证。显然，对角矩阵的特征值就等于其对角线上的元素。特别地，阶单位阵的特征值是，且该特征值对应的特征向量就是维空间的个坐标轴方向。

我们可以从线性变换的角度来理解矩阵的特征值和特征向量。一个阶方阵可以看作是维空间中的变换，将维向量变为另一个维向量。由于以及对任意向量和实数成立，该变换是一个线性变换。事实上，当坐标轴确定之后，线性变换与矩阵之间有一一对应关系。如果把向量都看作从原点指向向量所表示坐标的有向线段，可以证明，任意一个线性变换总可以分解成绕原点旋转和长度伸缩的组合。因此，矩阵与向量相乘可以理解为将向量旋转某一角度，再将长度变为某一倍数。而矩阵的特征向量，就是在该变换作用下只伸缩不旋转的向量，并且其对应的特征值就是伸缩的倍数。当特征值时，变换后的向量与原向量方向相同；时方向相反；则表示矩阵会把所有该直线上的向量压缩为零向量。

从这一角度继续，我们可以引入正定（positive definite）矩阵和半正定（positive semidefinite）矩阵的概念。如果对任意非零向量，都有，就称为半正定矩阵；如果严格有，就称为正定矩阵。如果将看作变换后的向量，那么就表示与之间的夹角小于等于90。由此，我们可以立即得到半正定矩阵的所有特征值都非负，否则负特征值会使特征向量在变换后反向，与原向量夹角为180，产生矛盾。

为什么我们要引入半正定矩阵呢？在上面的优化问题中，我们得到的目标函数是，其中是协方差矩阵。事实上，该矩阵一定是半正定矩阵。设是任一非零向量，那么：

根据定义，是半正定矩阵。因此，我们可以用半正定矩阵的一些性质来帮助我们求解该优化问题。这里，我们不加证明地给出一条重要性质：对于阶对称半正定矩阵，总可以找到它的个单位特征向量，使得这些特征向量是两两正交的，也即对任意，都有：

有兴趣的读者可以在线性代数的相关资料中找到该性质的证明。利用该性质，记，有：

于是，对角线上的元素全部为，其他元素全部为，恰好是单位矩阵。因此，的逆矩阵就是其转置，。因为组成该矩阵的向量是相互正交的，我们将这样的矩阵称为正交矩阵（orthogonal matrix）。根据逆矩阵的性质，我们有:

设特征向量对应的特征值是，那么矩阵可以写为：

其中，是由特征向量所对应的特征值依次排列而成的对角矩阵。上式表明，一个半正定矩阵可以分解成3个矩阵的乘积，其中是其正交的特征向量构成的正交矩阵，是其特征值构成的对角矩阵，这样的分解就称为矩阵的特征分解。

利用特征分解，我们可以很容易地计算的值。首先，由于是维空间中的个正交向量，一定可以唯一表示成这些向量的线性组合，即，其中系数等于向量在方向上的投影长度。我们可以将这组向量想象成相互垂直的坐标轴，而就相当于在这组坐标轴下的坐标。这样，可以化为：

这里，我们用到了的性质，把求和中都消去了。接下来，可以计算得：

在上面的优化问题中，我们还要求是方向向量，即。这一要求给系数添加了限定条件：

因此，原优化问题等价于：

由于是半正定矩阵，其特征值必定非负，该问题的解就是的最大特征值，不妨设其为。为了使上式取到最大值，应当有，且其他的全部为零。因此，使方差最大的方向就是该特征值对应的特征向量的方向。

上面的计算结果表面，用PCA寻找第一个主成分的过程就是求解PCA最大特征值及其对应特征向量的过程。事实上，由于协方差矩阵半正定，其所有特征向量正交，恰好也满足我们最开始“每个主成分都与之前的所有主成分正交”的要求。如果排除掉第一主成分，第二主成分就对应第二大特征值的特征向量，依次类推。因此，如果我们要把维的数据降到维，只需要计算最大的个特征值对应的特征向量即可。设这个特征向量依次为，矩阵，原数据矩阵，那么降维后的数据为：

15.3 动手实现PCA算法

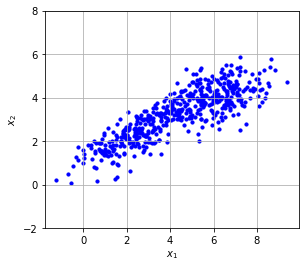
下面，我们在NumPy库中线性代数工具的帮助下实现PCA算法。首先，我们导入数据集PCA_dataset.csv并将其可视化。数据集的每一行包含两个数与，代表平面上点的坐标。

import numpy as np
import matplotlib.pyplot as plt

# 导入数据集
data = np.loadtxt('PCA_dataset.csv', delimiter=',')
print('数据集大小：', len(data))

# 可视化
plt.figure()
plt.scatter(data[:, 0], data[:, 1], color='blue', s=10)
plt.axis('square')
plt.ylim(-2, 8)
plt.grid()
plt.xlabel(r'$x_1$')
plt.ylabel(r'$x_2$')
plt.show()

数据集大小： 500

接下来，我们按上面讲解的方式实现PCA算法。numpy.linalg中提供了许多线性代数相关的工具，可以帮助我们计算矩阵的特征值与特征向量。

def pca(X, k):
    d, m = X.shape
    if d < k:
        print('k应该小于特征数')
        return X, None

    # 中心化
    X = X - np.mean(X, axis=0)
    # 计算协方差矩阵
    cov = X.T @ X
    # 计算特征值和特征向量
    eig_values, eig_vectors = np.linalg.eig(cov)
    # 获取最大的k个特征值的下标
    idx = np.argsort(-eig_values)[:k]
    # 对应的特征向量
    W = eig_vectors[:, idx]
    # 降维
    X = X @ W
    return X, W

最后，我们在数据集上测试该PCA函数的效果，并将变换后的数据绘制出来。由于原始数据只有二维，为了演示PCA的效果，我们仍然设置，不进行降维。但是，从结果中仍然可以看出PCA计算的主成分方向。相比于原始数据，变换后的数据最“长”的方向变成了横轴的方向。

X, W = pca(data, 2)
print('变换矩阵：\n', W)

# 绘图
plt.figure()
plt.scatter(X[:, 0], X[:, 1], color='blue', s=10)
plt.axis('square')
plt.ylim(-5, 5)
plt.grid()
plt.xlabel(r'$x_1$')
plt.ylabel(r'$x_2$')
plt.show()

变换矩阵：
 [[ 0.90322448 -0.42916843]
 [ 0.42916843  0.90322448]]

15.4 用sklearn实现PCA算法

Sklearn库中同样提供了实现好的PCA算法，我们可以直接调用它来完成PCA变换。可以看出，虽然结果图像与我们上面直接实现的版本有180的旋转，变换矩阵的元素也互为相反数，但PCA本质上只需要找到主成分的方向，因此两者得到的结果是等价的。

from sklearn.decomposition import PCA

# 中心化
X = data - np.mean(data, axis=0)
pca_res = PCA(n_components=2).fit(X)
W = pca_res.components_.T
print ('sklearn计算的变换矩阵：\n', W)
X_pca = X @ W

# 绘图
plt.figure()
plt.scatter(X_pca[:, 0], X_pca[:, 1], color='blue', s=10)
plt.axis('square')
plt.ylim(-5, 5)
plt.grid()
plt.xlabel(r'$x_1$')
plt.ylabel(r'$x_2$')
plt.show()

sklearn计算的变换矩阵：
 [[-0.90322448  0.42916843]
 [-0.42916843 -0.90322448]]

15.5 本章小结

本章介绍了数据降维的常用算法之一：PCA算法。数据降维是无监督学习的重要问题，在机器学习中有广泛的应用。由于从现实生活中采集的数据往往非常复杂，包含大量的冗余信息，通常我们必须对其进行降维，选出有用的特征供给后续模型使用。此外，有时我们还希望将高维数据可视化，也需要从数据中挑选2到3个最有价值的维度，将数据投影后绘制出来。除了PCA之外，现在常用的降维算法还有线性判别分析（linear discriminant analysis，LDA）、一致流形逼近与投影（uniform manifold approximation and projection，UMAP）、t分布随机近邻嵌入（t-distributed stochastic neighbor embedding，t-SNE）等。这些算法的特点各不相同，也有不同的适用场景。

关于PCA的计算方式，由于计算协方差矩阵和特征分解的时间复杂度较高，实践中通常会采用矩阵的奇异值分解（singular value decomposition，SVD）来代替特征分解。上面我们用到的sklearn库中的PCA算法就是以奇异值分解为基础的实现的。相比于特征分解，奇异值分解不需要实际计算出，并且存在更高效的迭代求解方法。感兴趣的读者可以查阅相关资料，了解特征分解和奇异值分解的异同。

最后，读者可以在SETOSA网站的PCA算法动态展示平台上观察PCA的结果随数据分布的变化，加深对算法的理解。

习题

1. PCA算法成立的的条件与数据分布的形式是否有关系？尝试计算下列特殊数据分布的第一个主成分，和你的直观感受一样吗？

   • 直线上的点；
   • 两边不等长的十字形；
   • 三维中单位立方体的个顶点。

2. 当有数据集中包含多个不同类别的数据时，PCA还可以用来把数据区分开，完成类似于聚类的效果。这样做的原理是什么？（提示：考虑主成分与方差的关系。）

3. 利用sklearn库中的sklearn.datasets.load_iris()函数加载鸢尾花数据集。该数据集中共包含3种不同的鸢尾花，每一行代表一朵鸢尾花，并给出了花萼长度、花瓣长度等特征，以及鸢尾花所属的种类。用PCA把其中的特征数据降到两维，画出降维后数据的分布，并为每种鸢尾花涂上不同颜色。不同种的样本是否被分开了？